A resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
2ER2R+r
ER2R+r
ER2R+r
2ERR+2r
The correct Answer is:A
To find the potential drop across the resistor R connected to a parallel combination of two identical batteries, we can follow these steps:
Step 1: Understand the Circuit Configuration
We have two identical batteries, each with an EMF E and internal resistance r, connected in parallel. The external resistor R is connected across this parallel combination.
Step 2: Calculate the Equivalent EMF of the Batteries
For two identical batteries in parallel, the equivalent EMF Eeq remains the same as the individual EMF:
Eeq=E
Step 3: Calculate the Equivalent Internal Resistance
The internal resistances of the two batteries in parallel combine as follows:
req=r2
Step 4: Set Up the Circuit with Equivalent Values
Now, we can represent the circuit with the equivalent EMF and equivalent internal resistance:
- EMF: Eeq=E
- Internal Resistance: req=r2
The circuit now looks like this:
- A battery with EMF E and internal resistance r2 in series with the resistor R.
Step 5: Calculate the Total Resistance in the Circuit
The total resistance Rtotal in the circuit is the sum of the equivalent internal resistance and the external resistance:
Rtotal=R+req=R+r2
Step 6: Calculate the Current I in the Circuit
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=EeqRtotal=ER+r2
Step 7: Calculate the Potential Drop Across the Resistor R
The potential drop VR across the resistor R can be calculated using Ohm's law:
VR=I⋅R=(ER+r2)⋅R
Substituting the value of I:
VR=E⋅RR+r2
Step 8: Simplify the Expression
To simplify the expression, we can multiply the numerator and denominator by 2:
VR=2ER2R+r
Final Result
The potential drop across the resistor R is:
VR=2ER2R+r
---
We have two identical batteries, each with an EMF E and internal resistance r, connected in parallel. The external resistor R is connected across this parallel combination.
For two identical batteries in parallel, the equivalent EMF Eeq remains the same as the individual EMF:
Eeq=E
The internal resistances of the two batteries in parallel combine as follows:
req=r2
Now, we can represent the circuit with the equivalent EMF and equivalent internal resistance:
- EMF: Eeq=E
- Internal Resistance: req=r2
- A battery with EMF E and internal resistance r2 in series with the resistor R.
The total resistance Rtotal in the circuit is the sum of the equivalent internal resistance and the external resistance:
Rtotal=R+req=R+r2
Using Ohm's law, the current I flowing through the circuit can be calculated as:
I=EeqRtotal=ER+r2
The potential drop VR across the resistor R can be calculated using Ohm's law:
VR=I⋅R=(ER+r2)⋅R
Substituting the value of I:
VR=E⋅RR+r2
To simplify the expression, we can multiply the numerator and denominator by 2:
VR=2ER2R+r
The potential drop across the resistor R is:
VR=2ER2R+r
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-2)
16 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-2 (Part-3)
22 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise-1 (Part-3)
2 Videos
- COMMUNICATION SYSTEMSBOOK - RESONANCECHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 3
13 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP.No.71
1 Video
Similar Questions
Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure

View SolutionThree resistors 1Ω,2Ω and 3Ω are combined in series. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
View Solution
Knowledge Check
A capacitor is conneted to a cell emf E having some internal resistance r. The potential difference across the
ACell is <EBCell is ECCapacitor is >EDCapacitor is <EThree resistances 2Ω,4Ω,5Ω are combined in series and this combination is connected to a battery of 12 V emf and negligible internal resistance. The potential drop across these resistances are
A(5,45,4.36,2.18)VB(2,18,5.45,4.36)VC(4.36,2.18,5.45)VD(2.18,4.36,5.45)VTo get the maximum current from a parallel combination of n identical cells each of internal resistance r in an external resistance R, when
AR>>rBR<<rCR=rDNone of these
(a) Three resistors 1Ω,2Ωand3Ω are combined in series. What is the total resistance of the combination ?
(b) If the combination is connected to a battery of emf 12 V and negligible internal resistance, obtain the potential drop across each resistor.
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure

View SolutionSeven identical cells each of e.m.f. E and internal resistance r are connected as shown . The potential difference between A and B is
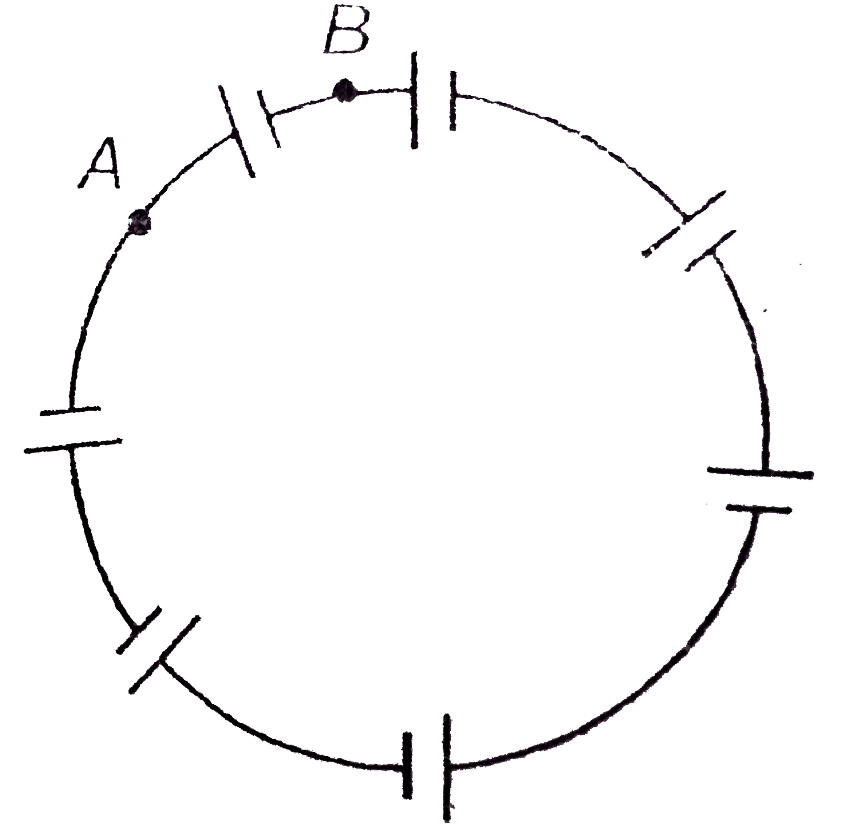
View SolutionTwo cells of same emf ε but of different internal resistances r1 and r2 are connected in series with an external resistance R. The potential drop across the first cell is found to be zero. The external resistance R is
View SolutionWhen galvanometer of unknown resistance connected across a series combination of two identical batteries each of 1.5 V, the current through the resistor is 1A. When it is connected across parallel combination of the same batteries, the current through it is 0.6 A. The internal resistance of each battery is
View Solution