Question

A parallel plate capacitor has a dielectric slab in it. The slab just fills the space inside the capacitor. The capacitor is charged by a battery and the battery is disconnected . Now the slab is started to pull out uniformly at t = 0. If at time t, capacitance of the capacitor is C, potential difference across plate is V, and energy stored in it is U, then which of the following graphs are correct ?

Options

A.
B.
C.
D.

Answer

A::B::C::D

Explanation

To solve the problem regarding the behavior of a parallel plate capacitor with a dielectric slab being pulled out, we will analyze the relationships between capacitance (C), potential difference (V), and energy stored (U) in the capacitor over time.

1. Understanding the Initial Conditions:
- Initially, the capacitor has a dielectric slab with a dielectric constant \( K \). The capacitance of the capacitor can be expressed as:
\( C = K \cdot \frac{\epsilon_0 A}{d} \)
- Here, \( \epsilon_0 \) is the permittivity of free space, \( A \) is the area of the plates, and \( d \) is the separation between the plates.

2. When the Dielectric is Pulled Out:
- As the dielectric slab is pulled out uniformly, the dielectric constant \( K \) effectively decreases, leading to a decrease in capacitance \( C \). When the slab is completely removed, the capacitance becomes:
\( C_0 = \frac{\epsilon_0 A}{d} \)
- Thus, the relationship between the capacitance with and without the dielectric is:
\( C = K \cdot C_0 \)
- As \( K \) decreases, \( C \) also decreases over time.

3. Relationship Between Charge, Capacitance, and Voltage:
- Since the capacitor is charged and then disconnected from the battery, the charge \( Q \) on the capacitor remains constant. The relationship between charge, capacitance, and voltage is given by:
\( Q = C \cdot V \)
- Rearranging gives us:
\( V = \frac{Q}{C} \)
- As capacitance \( C \) decreases, the potential difference \( V \) across the capacitor must increase since \( Q \) is constant.

4. Energy Stored in the Capacitor:
- The energy \( U \) stored in the capacitor is given by:
\( U = \frac{1}{2} C V^2 \)
- Since \( V \) increases as \( C \) decreases, we can analyze how \( U \) changes. As \( C \) decreases, the energy stored will also change, but the exact relationship will depend on the specific values of \( C \) and \( V \).

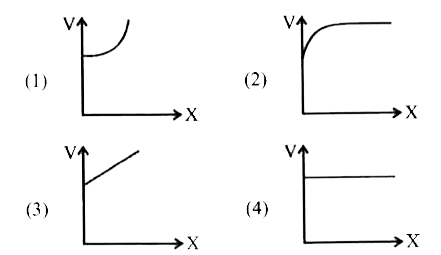
5. Graphical Representation:
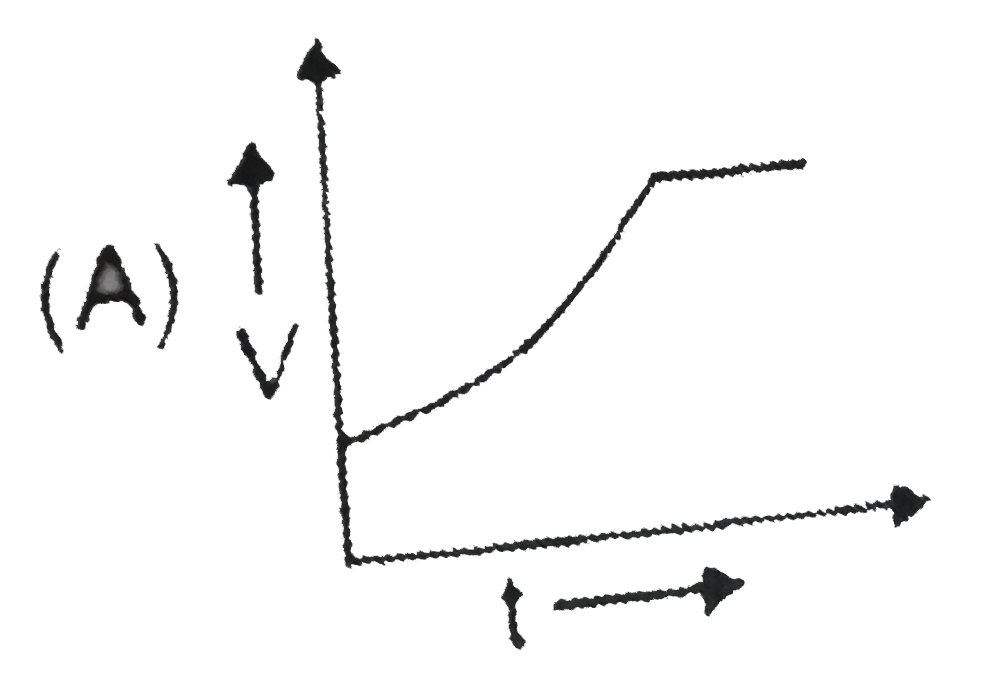
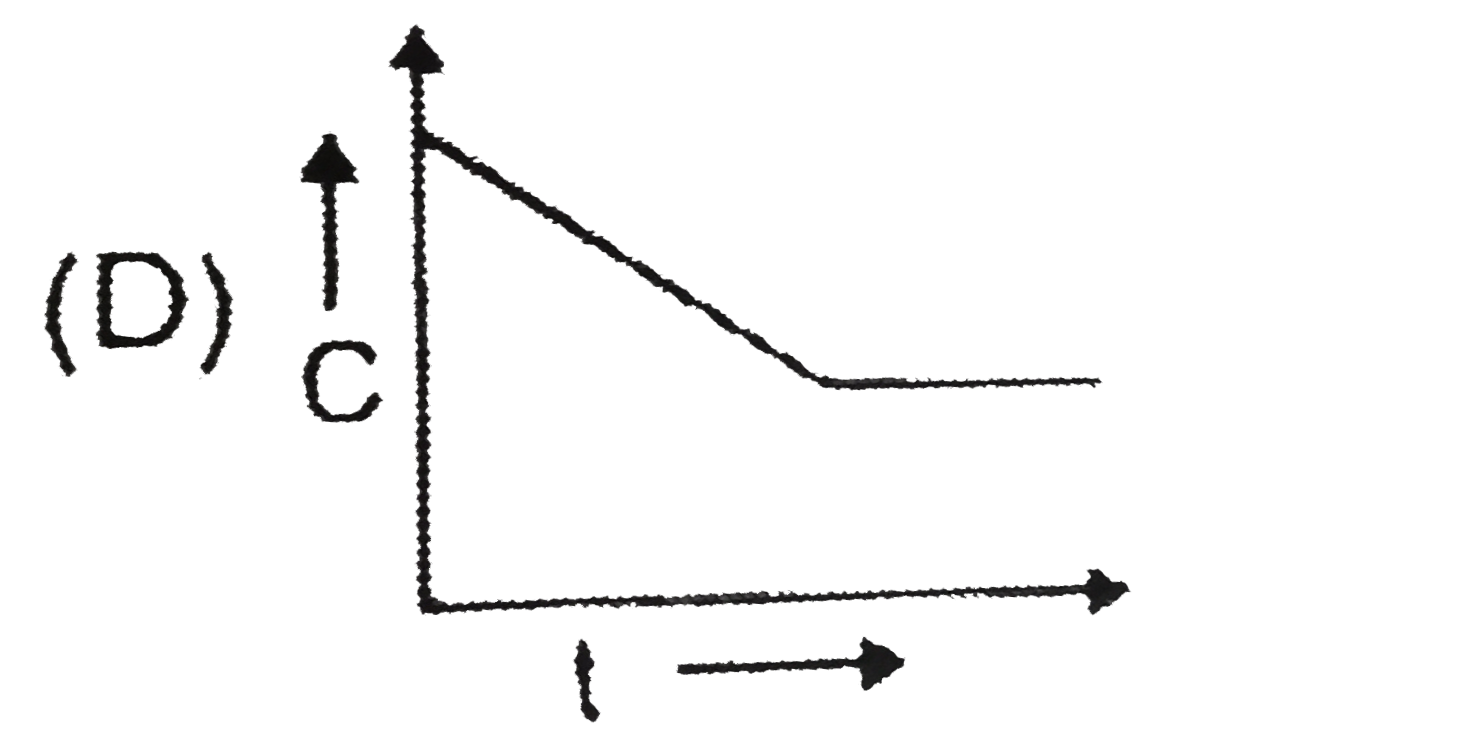
- Capacitance vs. Time (C vs. t): This graph will show a decreasing trend as the dielectric is pulled out.
- Potential vs. Time (V vs. t): This graph will show an increasing trend as the capacitance decreases.
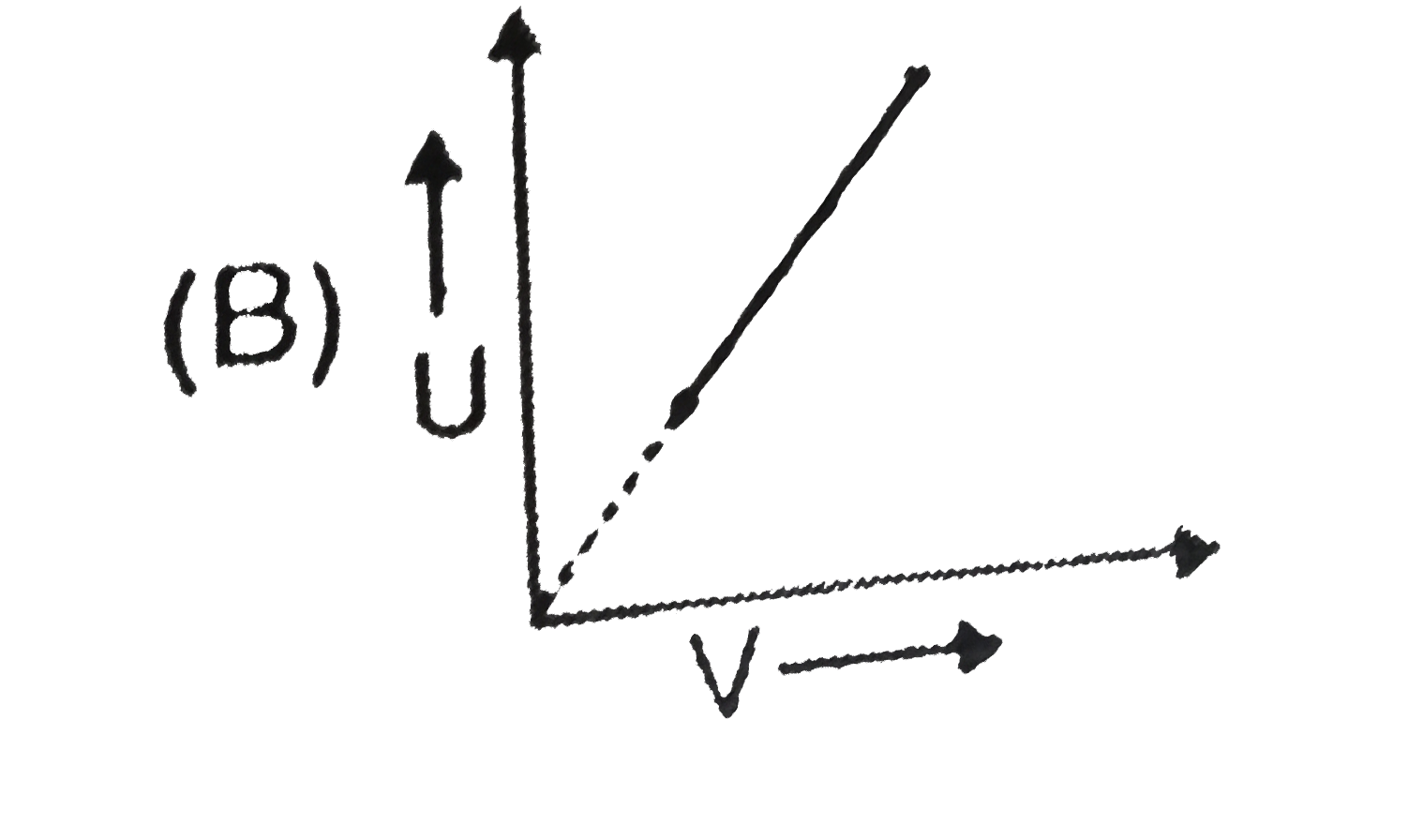
- Energy vs. Potential (U vs. V): This graph will show a quadratic relationship since \( U \) is proportional to \( V^2 \).
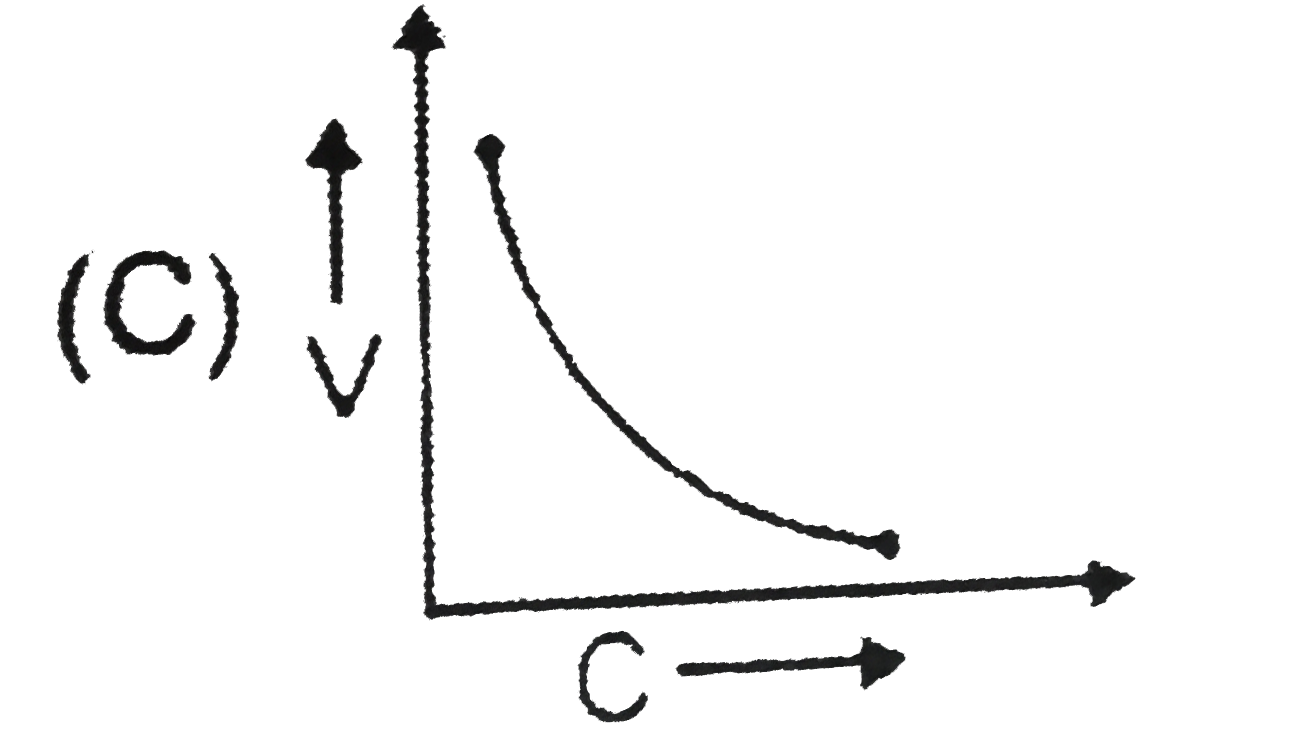
- Potential vs. Capacitance (V vs. C): This graph will show an inverse relationship since \( V \) is inversely proportional to \( C \).

Conclusion:
Based on the analysis, all four graphs representing the relationships between capacitance, potential, and energy are correct.