A capacitor of capacitance 10μF is charged to a potential 50V with a battery. The battery is now disconnected and an additional charge 200μC is given to the positive plate of the capacitor. The potential difference across the capacitor will be.
50 V
80 V
100 V
60 V
The correct Answer is:D
To solve the problem step by step, we will follow the outlined process below:
Step 1: Calculate the initial charge on the capacitor
The capacitance C of the capacitor is given as 10μF (microfarads), and the potential difference V is 50V.
Using the formula for charge Q:
Q=C×V
Substituting the values:
Q=10×10−6F×50V=500μC
Step 2: Add the additional charge to the positive plate
An additional charge of 200μC is given to the positive plate of the capacitor. Therefore, the total charge on the positive plate becomes:
Qtotal=500μC+200μC=700μC
Step 3: Determine the charge on the negative plate
Since the capacitor is isolated (the battery is disconnected), the charge on the negative plate remains unchanged at −500μC.
Step 4: Calculate the net charge on the capacitor
The net charge on the capacitor is the charge on the positive plate minus the charge on the negative plate:
Qnet=Qpositive−Qnegative=700μC−(−500μC)=700μC+500μC=1200μC
Step 5: Calculate the potential difference across the capacitor
Using the formula for potential difference V:
V=QC
Substituting the values:
V=1200μC10μF=1200×10−6C10×10−6F=120V
Final Answer
The potential difference across the capacitor will be 120V.
---
The capacitance C of the capacitor is given as 10μF (microfarads), and the potential difference V is 50V.
Q=C×V
Substituting the values:
Q=10×10−6F×50V=500μC
An additional charge of 200μC is given to the positive plate of the capacitor. Therefore, the total charge on the positive plate becomes:
Qtotal=500μC+200μC=700μC
Since the capacitor is isolated (the battery is disconnected), the charge on the negative plate remains unchanged at −500μC.
The net charge on the capacitor is the charge on the positive plate minus the charge on the negative plate:
Qnet=Qpositive−Qnegative=700μC−(−500μC)=700μC+500μC=1200μC
Using the formula for potential difference V:
V=QC
Substituting the values:
V=1200μC10μF=1200×10−6C10×10−6F=120V
The potential difference across the capacitor will be 120V.
Topper's Solved these Questions
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:NCERT Based
Explore 13 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Level-V
Explore 35 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Level-II (C.W)
Explore 14 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
Similar Questions
A capacitor having a capacitance of 200 μF is charged to a potential difference of 20V. The charging battery is disconnected and the capacitor is connected to another battery of emf 10V with the positive plate of the capacitor joined with the positive terminal of the battery.
(a) Find the charges on the capacitor before and after the reconnection in steady state.
(b) Find the net charge flown through the 10 V battery
Is work done by the battery or is it done on the battery? Find its magnitude.
(d) Find the decrease in electrostatic field energy.
(e) Find the heat developed during the flow of charge after reconnection .
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View Solution
Knowledge Check
Two capacitors of capacitance 2μF and 4μF respectively are charged to a potential of 12 V. they are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each capacitor will be
A2 VB3VC4VD6VA capacitor of capacitance C is charged to a potential difference V from a cell and then disconnected from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
AVBV+QCCV+Q2CDV−QC, if V<CVA capacitor of capacitance C is charged to a potential difference V from a cell and then disconnected from it. A charge +Q is now given to its positive plate. The potential difference across the capacitor is now
AVBV+QCCV+Q2CDV−QC if Q<CV
Two parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionA 100pF capacitor is charged to a potential difference of 80.0V and the charging battery is disconnected. The capacitor is then connected in parallel with a second capacitor. If the potential difference across the first capacitor drops to 35.0 V what is the capacitance of this second capacitor?
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionA 10V battery is connected to two capacitors C1 and C2 and a resistor R. When the capacitors are fully charged, then the potential difference across the resistor will be
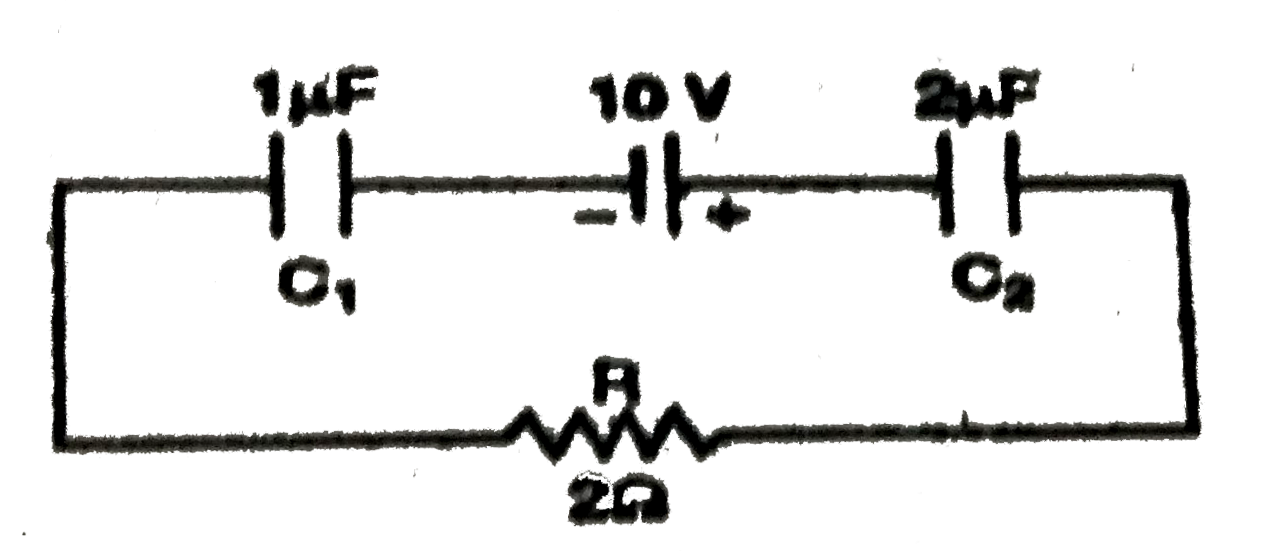
View SolutionA capacitor of capacitnace C is charged to a potential difference V and then disconnected from the battery. Now it is connected to an inductor of inductance L at t=0. Then

View Solution

