A condenser of capacity 500μF is charged at the rate of 400μF per second. The time required to raise its potential by 40V is.
50 s
100 s
20 s
10 s
The correct Answer is:A
To solve the problem, we need to determine the time required to raise the potential of a capacitor (condenser) with a given capacitance when charged at a specific rate.
1. Understand the relationship between charge, capacitance, and voltage:
The relationship is given by the formula:
Q=C⋅V
where Q is the charge in coulombs, C is the capacitance in farads, and V is the voltage in volts.
2. Identify the given values:
- Capacitance, C=500μF=500×10−6F
- Rate of charging, dQdt=400μC/s=400×10−6C/s
- Desired increase in voltage, dV=40V
3. Relate charge change to voltage change:
From the formula Q=C⋅V, we can differentiate both sides with respect to time t:
dQdt=C⋅dVdt
4. Substitute the known values into the equation:
400×10−6=500×10−6⋅dVdt
5. Solve for dVdt:
Rearranging the equation gives:
dVdt=400×10−6500×10−6=400500=0.8V/s
6. Calculate the time required to raise the potential by 40 V:
Using the relationship dV=dVdt⋅dt:
dt=dVdVdt=40V0.8V/s=50s
Final Answer:
The time required to raise the potential by 40 V is 50 seconds.
---
The relationship is given by the formula:
Q=C⋅V
where Q is the charge in coulombs, C is the capacitance in farads, and V is the voltage in volts.
- Capacitance, C=500μF=500×10−6F
- Rate of charging, dQdt=400μC/s=400×10−6C/s
- Desired increase in voltage, dV=40V
From the formula Q=C⋅V, we can differentiate both sides with respect to time t:
dQdt=C⋅dVdt
400×10−6=500×10−6⋅dVdt
Rearranging the equation gives:
dVdt=400×10−6500×10−6=400500=0.8V/s
Using the relationship dV=dVdt⋅dt:
dt=dVdVdt=40V0.8V/s=50s
The time required to raise the potential by 40 V is 50 seconds.
Topper's Solved these Questions
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:NCERT Based
Explore 13 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Level-V
Explore 35 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Level-II (C.W)
Explore 14 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
Similar Questions
A capacitor of 8μF is charged to a potential of 1000V.The energy stored in the capacitor is ......
View SolutionConsider the circuit shown with key opened. Capacitor -1 ( 3μF) is charged to potential difference of 9V Capacitor -2 (6μF) is charged to potential difference of 3V. The key is now closed . What will be the potential difference ( in V) across capacitor-1 in steady state ?
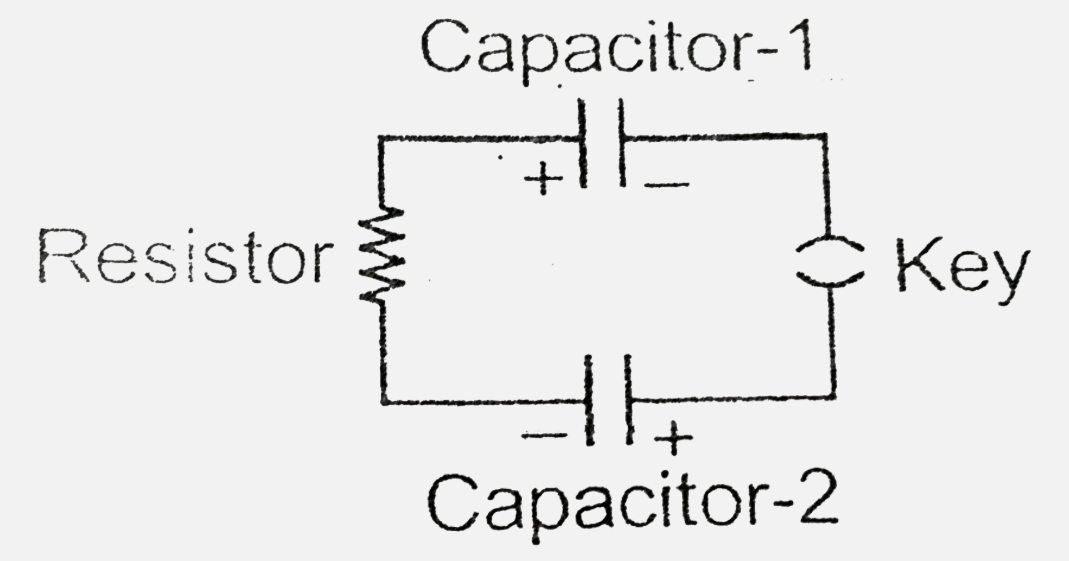
View Solution
Knowledge Check
A condenser of capacity 50μF is charged to 10 volts. Its energy is equal to
A2.5×10−3JB2.5×10−4JC5×10−2JD1.2×108JA parallel plate air condenser of capacity 10μF is charged to a potential of 1000V. The energy of the condenser is
A5 JB4 JC2.5 JD10 JA condenser of capacity 40μF is cahrged to a potential of 1 KV. What is the work done in raising the potential ?
A5 JB10 JC20 JD30 J
A capacitor of capacity 2μF is charged to a potential difference of 12V. It is then connected across an inductor of inductance 6μH. What is the current (in A) in the circuit at a time when the potential difference across the capacitor is 6.0V?
View SolutionA condenser of capacity 10μF is charged to a potential of 500V. Its terminals are then connected to those of an uncharged condenser of capacity 40μF. The loss of energy in connecting them together is.
View SolutionA parallel plate air condenser of capacity 4μF is charged to a potential of 1000 V. the energy of the condenser is
View SolutionA condenser of capacity 20μF is first charged and then discharged through a 10mH inductance. Neglecting the resistance of the coil, the frequency of the resulting vibrations will be
View SolutionA condenser of of capacity 2μF is charged to a potential of 100V. It is now connected to an uncharged condenser of capacity 3μF . The common potential will be
View Solution

