A parallel plate condenser has initially air medium between the plates. If a slab of dielectric constant 5 having thickness half the distance of separation between the plates is introduced, the percentage increase in its capacity is.
33.3%
66.7%
0.5
0.75
The correct Answer is:B
To solve the problem of finding the percentage increase in the capacitance of a parallel plate capacitor when a dielectric slab is introduced, we can follow these steps:
Step 1: Determine the initial capacitance (C₀)
The capacitance of a parallel plate capacitor with air (or vacuum) as the dielectric medium is given by the formula:
C0=Aϵ0D
Where:
- C0 = initial capacitance
- A = area of the plates
- ϵ0 = permittivity of free space
- D = distance between the plates
Step 2: Introduce the dielectric slab
When a dielectric slab of thickness t=D2 and dielectric constant K=5 is introduced between the plates, the capacitor can be considered as two capacitors in series:
1. The first capacitor has the dielectric slab with thickness t=D2.
2. The second capacitor has air with thickness D−t=D2.
Step 3: Calculate the capacitance with the dielectric slab (C')
The capacitance of the first part (with the dielectric) is:
C1=AKϵ0t=A⋅5ϵ0D2=10Aϵ0D
The capacitance of the second part (with air) is:
C2=Aϵ0D−t=Aϵ0D2=2Aϵ0D
Step 4: Find the total capacitance (C')
Since the two capacitances are in series, the total capacitance C′ can be calculated using the formula for capacitors in series:
1C′=1C1+1C2
Substituting the values:
1C′=110Aϵ0D+12Aϵ0D
This simplifies to:
1C′=D10Aϵ0+D2Aϵ0
Finding a common denominator (10Aε₀):
1C′=D10Aϵ0+5D10Aϵ0=6D10Aϵ0=3D5Aϵ0
Thus,
C′=5Aϵ03D
Step 5: Calculate the percentage increase in capacitance
Now, we can find the percentage increase in capacitance:
Percentage Increase=(C′−C0C0)×100
Substituting C′ and C0:
Percentage Increase=⎛⎜⎝5Aϵ03D−Aϵ0DAϵ0D⎞⎟⎠×100
This simplifies to:
=⎛⎝53−11⎞⎠×100=(23)×100=66.67%
Final Answer
The percentage increase in capacitance is 66.67%.
---
The capacitance of a parallel plate capacitor with air (or vacuum) as the dielectric medium is given by the formula:
- C0 = initial capacitance
- A = area of the plates
- ϵ0 = permittivity of free space
- D = distance between the plates
When a dielectric slab of thickness t=D2 and dielectric constant K=5 is introduced between the plates, the capacitor can be considered as two capacitors in series:
1. The first capacitor has the dielectric slab with thickness t=D2.
2. The second capacitor has air with thickness D−t=D2.
The capacitance of the first part (with the dielectric) is:
Since the two capacitances are in series, the total capacitance C′ can be calculated using the formula for capacitors in series:
Now, we can find the percentage increase in capacitance:
The percentage increase in capacitance is 66.67%.
Topper's Solved these Questions
- CAPACITANCEBOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-III (C.W)
41 Videos
- CAPACITANCEBOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - NCERT Based
13 Videos
- CAPACITANCEBOOK - NARAYNACHAPTER - CAPACITANCEEXERCISE - Level-I (C.W)
16 Videos
- ATOMS BOOK - NARAYNACHAPTER - ATOMS EXERCISE - EXERCISE -4
47 Videos
- COMMUNICATION SYSTEMBOOK - NARAYNACHAPTER - COMMUNICATION SYSTEMEXERCISE - Level-II(H.W)
25 Videos
Similar Questions
A parallel plate capacitor with air as the dielectric has capacitance C. A slab of dielectric constant K and having the same thickness as the separation between plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. The new capacitance will be :
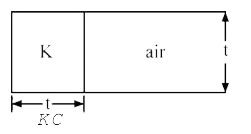
View SolutionA metal slab of thickness, equal to half the distance between the plates is introduced between the plates of a parallel plate capacitor as shown. Find its capacity.
 .
.
View Solution
Knowledge Check
parallel plate capacitor has capacitance C when no dielectric between thw plates. Now a slab of dielectric constant K, having same thickness as the separation between the plates is introduced so as to fill one-fourth of the capacitor as shown in the figure. the new capacitance will be
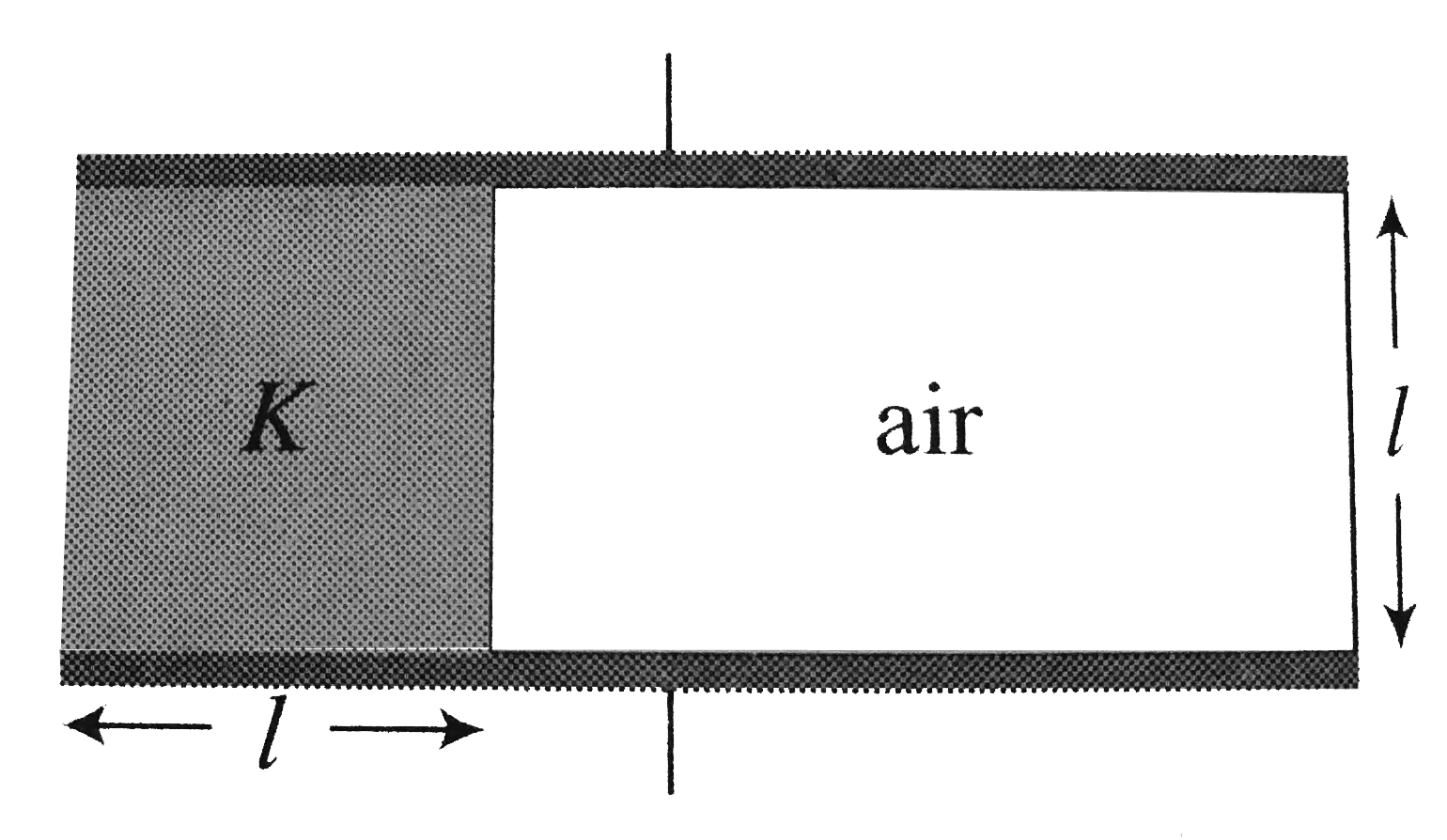 A(K+1)C4B(K+2)C4C(K+3)C4DKC4
A(K+1)C4B(K+2)C4C(K+3)C4DKC4A parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
AKC/2B2KC/(K+1)C2KC/(K−1)DC(K+1)/(K−1)The plates of a parallel plate capacitor with air as medium are separated by a distance of 8mm. A medium of dielectric constant 2 and thickness 4mm having the same area is introduced between the plates. For the capacitanace to remain the same, the distance between the plates is
A8mmB6mmC10mmD12mm
A parallel plate capacitor has the space between the plates filled with a medium whose dielecric constant increases uniformly with distance.Let d be the distance between the plates and K1 and K2 be the dielectric constant of the medium at the two plates ( square shaped with area A). Find the capacity of the capacitor.
View SolutionThe two plates of a parallel plate capacitor are 4 mm apart . A slab of dielectric constant 3 and thickness 3 mm is introduced between the plates with its face parallel to them . The distance between the plates is so adjusted that the capacity of the capacitor becomes 23 rd of its original value . What is the new distance the plates ?
View SolutionA parallel plate capacitor with air between the plates has a capacitance 2μF. The capacity of the condenser when the distance between the plates is reduced to half of initial distance is
View SolutionA dielectric introduced between the plates of parallel plate condenser
View SolutionA dielectric introduced between the plates of parallel plate condenser
View Solution
