Question

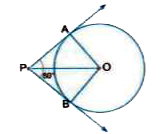
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of ${\displaystyle {80}^{\circ }}$, then ${\displaystyle \angle POA}$ is equal to

Explanation

To solve the problem step by step, we will analyze the given information and apply the properties of tangents and triangles.

Step 1: Understand the Problem
We have a circle with center O, and two tangents PA and PB drawn from point P to the circle. The angle between these tangents, ∠BPA, is given as 80 degrees. We need to find the angle ∠POA.

Step 2: Identify Relevant Properties
Recall that the radius of a circle is perpendicular to the tangent at the point of contact. Therefore:
- OA is perpendicular to AP, which means ∠OAP = 90 degrees.
- OB is perpendicular to BP, which means ∠OBP = 90 degrees.

Step 3: Analyze Triangles
Consider triangles POA and POB. Since OA and OB are both radii of the circle, we can establish the following:
- OA = OB (both are radii of the same circle)
- OP is common to both triangles.

Step 4: Use RHS Criterion
Since we have:
- ∠OAP = ∠OBP = 90 degrees
- OP is common
- OA = OB

We can conclude that triangles POA and POB are congruent by the RHS (Right angle-Hypotenuse-Side) criterion.

Step 5: Apply CPCT
From the congruence of triangles POA and POB, we can state that:
- ∠APO = ∠BPO (by CPCT)

Step 6: Calculate ∠APO
Given that ∠BPA = 80 degrees, we can express ∠APO as:
- ∠APO = 1/2 * ∠BPA = 1/2 * 80 degrees = 40 degrees.

Step 7: Use Triangle Sum Property
Now, consider triangle POA. The sum of angles in a triangle is 180 degrees:
- ∠POA + ∠OAP + ∠APO = 180 degrees.

Substituting the known values:
- ∠POA + 90 degrees + 40 degrees = 180 degrees.

Step 8: Solve for ∠POA
Now, we can solve for ∠POA:
- ∠POA + 130 degrees = 180 degrees
- ∠POA = 180 degrees - 130 degrees
- ∠POA = 50 degrees.

Final Answer
Thus, the angle ∠POA is equal to 50 degrees.

---