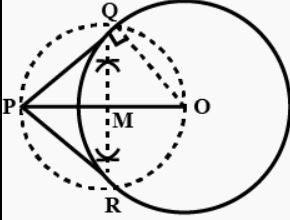
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Steps of Construction:
1. A circle with a radius of 6 cm is drawn taking O as the centre.
2. Point P is marked at 10 cm away from the centre of the circle.
3. With the half of compass mark M which is the midpoint of OP.
4. Draw a circle with centre M, taking radius MO or MP which intersects the given circle at Q and R.
5. Now join PQ and PR. These are the tangents of the circle.
We know that the tangent to a circle is perpendicular to the radius through the point of contact.
∴ In △OPQ, OQ⊥QP
and in △OPR, OR⊥PR
Hence, both △OPQ and △OPR are right-angle triangles.
Applying Pythagoras theorem to both △s, we get:
(OP)2=(OQ)2+(PQ)2
and (OP)2=(OR)2+(PR)2
OQ=OR=radius=6 cm and OP=10 cm
∴ 102=62+(PQ)2
and 102=62+(PR)2
⇒(PQ)2=100−36=64
and (PR)2=100−36=64
then, PQ=PR=8cm
Hence, the length of the tangents to a circle of radius 6 cm, from a point 10 cm away from the centre of the circle, is 8cm.
Topper's Solved these Questions
Similar Questions
Draw a circle of radius 4 cm. From the point 7 cm away from its centre, construct the pair of tangents to the circle.
View SolutionDraw a circle of radius 5 cm. From a point P, 8 cm away from its centre, construct a pair of tangents to the circle. Measure the length of each one of the tangents.
View SolutionDraw a circle of radius 3 cm. From a point 5 cm from the centre of the circle, draw two tangents to the circle. Measure the length of each tangent.
View SolutionDraw a circle of radius 2.5cm. Take a point P at a distance of 8 cm from its centre. Construct a pair of tangents from the point P to the circle.
View SolutionDraw two concentric circles of radii 3 cm and 5 cm. Taking a point on outer circle, construct the pair of tangents to the other. Measure the length of a tangent and verify is by actual calculation.
View SolutionDraw a circle of radius 3 cm. Take a point P on the circle. At point P, construct a tangent to the circle.
View SolutionDraw two circles of radii 6 cm and 4 cm. From a point on the outer circle, draw a tangent to the inner circle and measure its length.
View SolutionDraw two concentric circles of radii 3 cm and 5 cm . Taking a point on outer circle construct the pair of tangents to the other. Measure the length of a tangent and verify it by actual calculation .
View SolutionFrom a point Q, 13 cm away from the centre of a circle, the length of tangent PQ to the circle is 12 cm. The radius of the circle (in cm) is
View SolutionDraw a circle of radius 3 cm. Take a point P at a distance of 5 cm from the centre of the circle. From P, construct a pair of tangents to the circle.
View Solution
