Question

Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.

Explanation

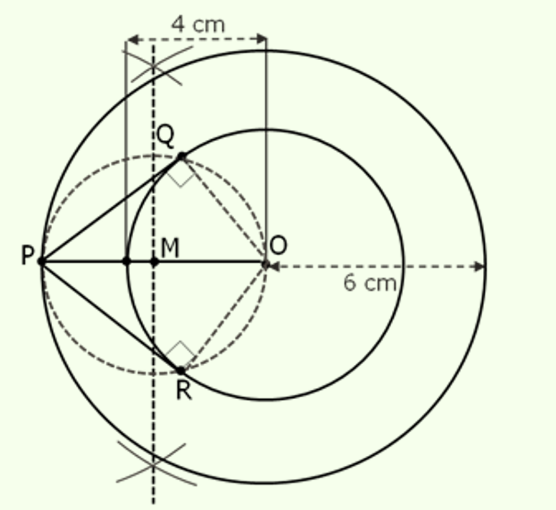
Steps of construction:


Take ‘O’ as centre and radius 4 cm and 6 cm respectively to draw two circles.


Take a point ‘P’ on the bigger circle and join OP.


With ‘O’ and ‘P’ as centre and radius more than half of OP draw arcs above and below OP to intersect at X and Y.


Join XY to intersect OP at M.


With M as centre and OM as radius draw a circle to cut the smaller circle at Q and R.


Join PQ and PR. PQ and PR are the required tangents, where PQ = PR = 4.5 cm (approx.)


Proof:


`∠PQO = 90^@`(Angle in a semi-circle)


`∴ PQ ⊥ OQ`



OQ is the radius of the smaller circle and PQ is the tangent at Q.


In the right ΔPQO,


OP = 6 cm (radius of the bigger circle)


OQ = 4 cm (radius of the smaller circle)


`(PQ)^2 = (OP)^2- (OQ)^2`


`= (6)^2 - (4)^2`



`= 36 - 16`



`= 20`



`PQ = sqrt20`



`= 4.5` (approx)


Similarly, we can prove `PR = 4.5 `(approx.)