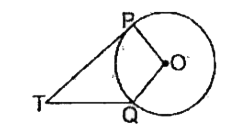
Two tangents TP and TQ are drawn to a circle with centre O from an external point T . Prove that ∠PTQ=2∠OPQ .
We know that, the lengths of tangents drawn from an external point to a circle are equal.
TP=TQ
In triangle TPQ,
TP = TQ
∠TQP=∠TPQ
(In a triangle, equal sides have equal angles opposite to them)
∠TQP+∠TPQ+∠PTQ=1800
(Angle sum property)
2∠TPQ+⋅∠PTQ=1800
∠PTQ=1800 - ∠TPQ
We know that, a tangent to a circle is perpendicular to the radius through the point of contact.
OP is perpendicular to PT
∠OPT=900
Thus,
∠PTQ = 2∠OPQ
Hence proved.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two tangents PA and PB are drawn to a circle with centre O from an external point P. If ∠OAB=30∘, then ∠APB is:
केंद्र O वाले वृत्त पर एक बाहरी बिंदु P से दो स्पर्श रेखाएँ PA तथा PB खींची जाती हैं | यदि ∠OAB=30∘ है, तो ∠APB का मान क्या होगा ?A15∘B30∘C120∘D60∘TP and TQ are tangents from T to the circle with centre O. Then is it possible to draw a circle through the points P, O, Q and T ?
 ANoBYesCCannot sayDData insufficient
ANoBYesCCannot sayDData insufficient
Two circles touch externally at a point P . From a point T on the tangent at P , tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ=TR . (FIGURE)
View SolutionFrom an external point P, two tangents PAandPB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
View SolutionIn the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT=30∘, prove that BA:AT =2:1
View SolutionIn Fig, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR=130∘ and S is a point on the circle, find ∠1+∠2.
View SolutionFrom any point P tangents of length t1 and t2 are drawn to two circles with centre A,B and if PN is the perpendicular from P to the radical axis and t21-t22=K.PN⋅AB then K=
View SolutionIf angle between two tangents drawn from a point P to a circle of radius 'a' and the centre O is 90∘ then prove that OP=√a
View Solution