The system shown in the figure is in equilibrium. Masses m1&m2 are 2kg and 8 kg respectively. The compression in right spring is 0.5 m. (Both spring have the same natural length) [K1=20N/m,K2=70N/m]. Choose the correct option(s) :
![The system shown in the figure is in equilibrium. Masses m(1) & m(2) are 2kg and 8 kg respectively. The compression in right spring is 0.5 m. (Both spring have the same natural length) [K(1)=20 N//m, K(2)=70 N//m]. Choose the correct option(s) :](https://d10lpgp6xz60nq.cloudfront.net/physics_images/VBA_RT_8_E01_450_Q01.png)
elongation in left spring is 0.5m
elongation in left spring is 0.25 m
Tension is string is 45 N
Just after left spring is cut m1, has upward acceleration.
The correct Answer is:C, D
F = 8t
mdvdt=8t
mv∫0dv=8t∫0tdt
mv=4t2
or mdxdt=4t2⇒dx=4t2mdt=2t2dt
W=∫Fdx=2∫0(8t×2t2)dt=64J
Topper's Solved these Questions
Similar Questions
Shown in the figure is a system of three particles having masses m1=1kg,m2=2kgand m1=4kg respectively connected by two springs. The accelartion of A, B and C at any instant are 1m/sec2,2m/sec2 and 1/2msec2 respectively directed as shown in the figure. the external force in N acting on the system is. . . ..
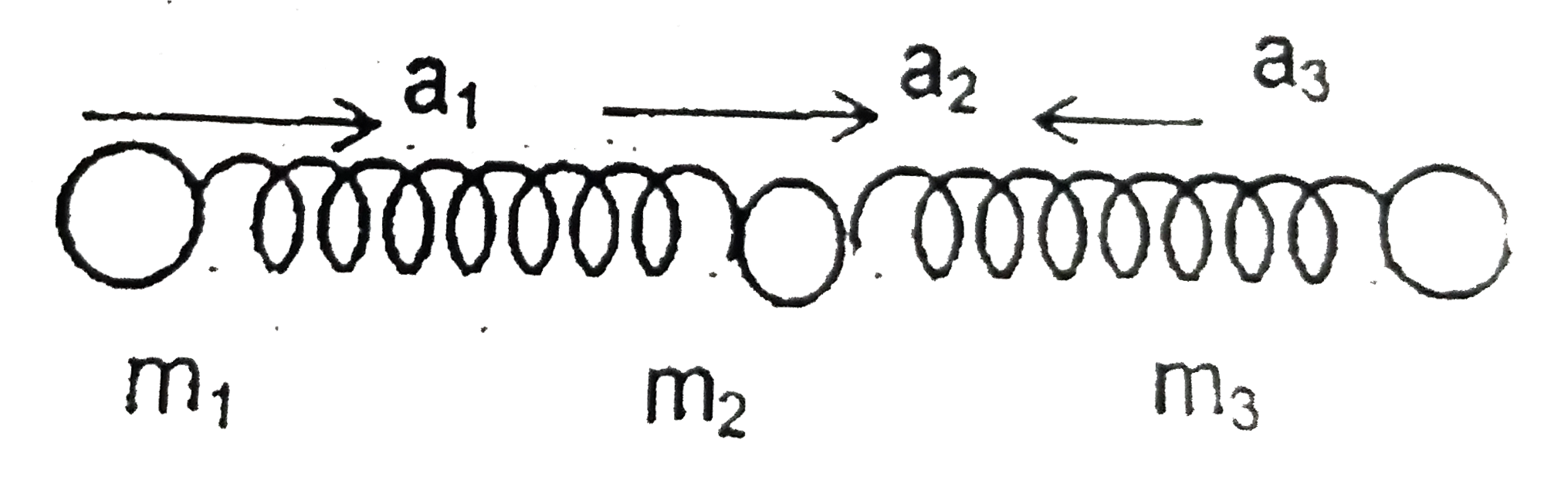
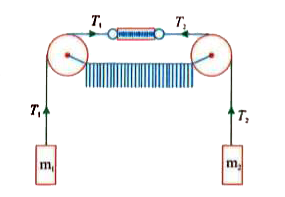
View SolutionTwo masses m1 and m2 are attached to a spring balance S as shown in Figure. If m1>m2 then the reading of spring balance will be
View Solution
Knowledge Check
The system shown in fig is in equilibrium . Masses m1andm2 are 2kg and 8kg, Respectively. Spring constants k1andk2 are 50Nm−1and70Nm−1, respectively. If the compression in second spring is 0.5m. What is the compression in first spring?
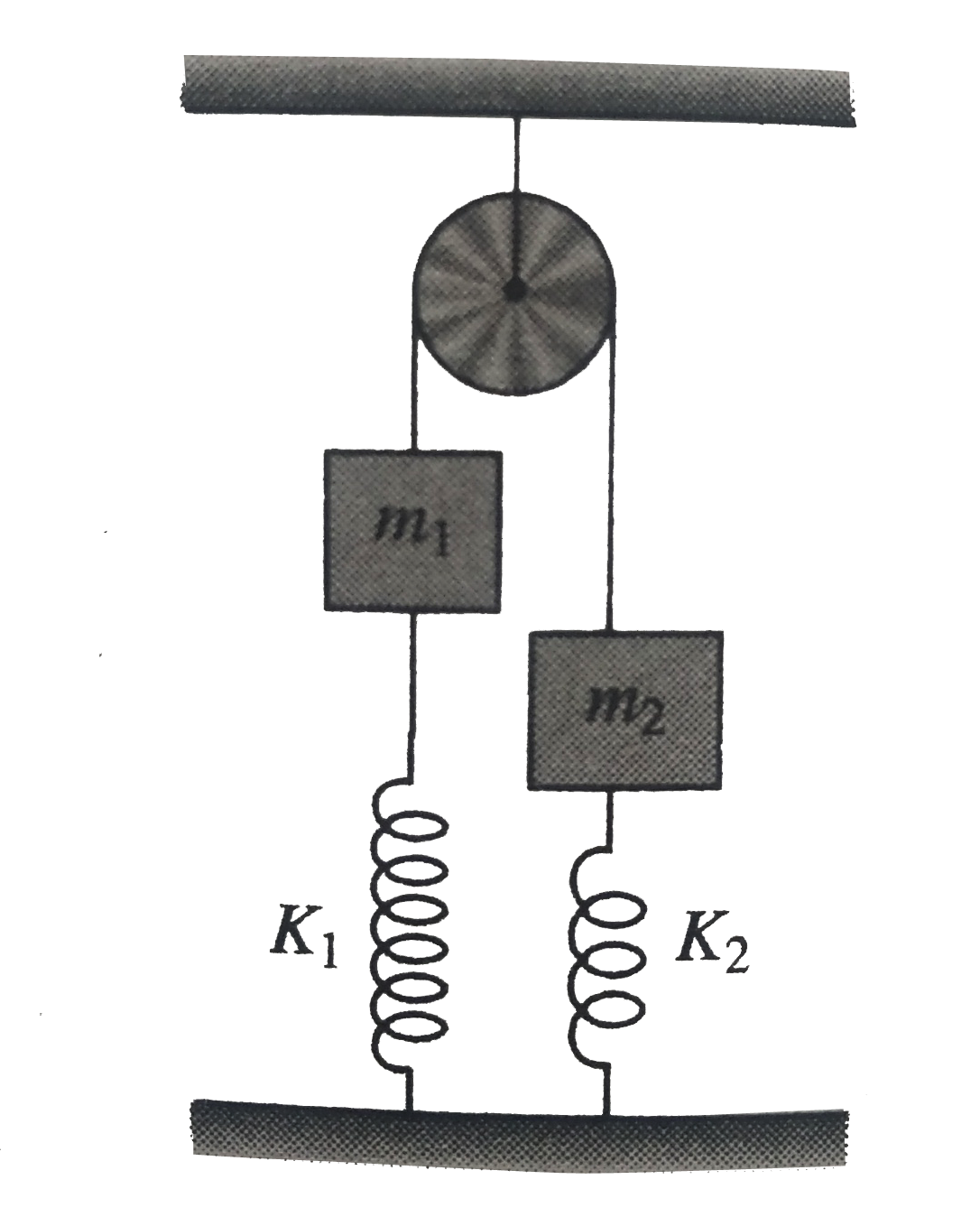 A1.3mB−0.5mC0.5mD0.9m
A1.3mB−0.5mC0.5mD0.9mFrom the fixed pulley, masses 2kg, 1kg and 3kg are suspended as shown in the figure. Find the extension in the spring if k=100N/m. (Neglect oscillations due to spring)
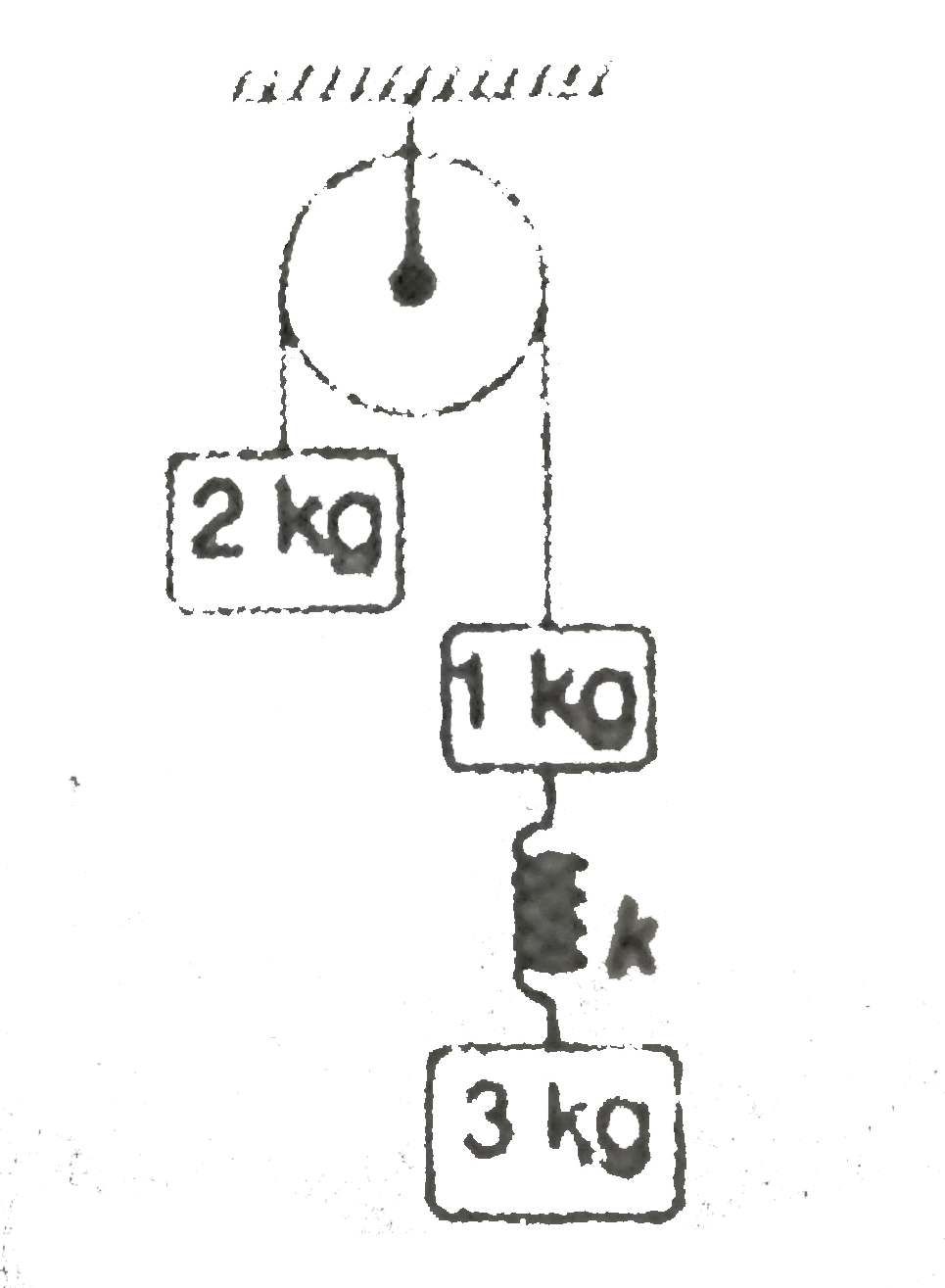 A0.1mB0.2mC0.3mD0
A0.1mB0.2mC0.3mD0Two masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
.A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
In the system as shown in figure, the blocks have masses m1 and m2, the spring constant is k, coefficient of friction between the block of mass m1 and the surface is μ. The system is released with zero initial speed from the position where the spring is in its natural length.

View SolutionIf the system is suspended by the mass m the length of the spring is l1. If it is inverted and hung by mass M, the length of the spring is l2. Find the natural length of the spring.

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When thye spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View SolutionThe two masses m1 and m2 are joined by a spring as shown. The system is dropped to the ground from a height. The spring will be

View SolutionTwo blocks of masses 1kg and 3kg are moving with velocities 2m/s and 1m/s , respectively , as shown. If the spring constant is 75N/m , the maximum compression of the spring is

View Solution