A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
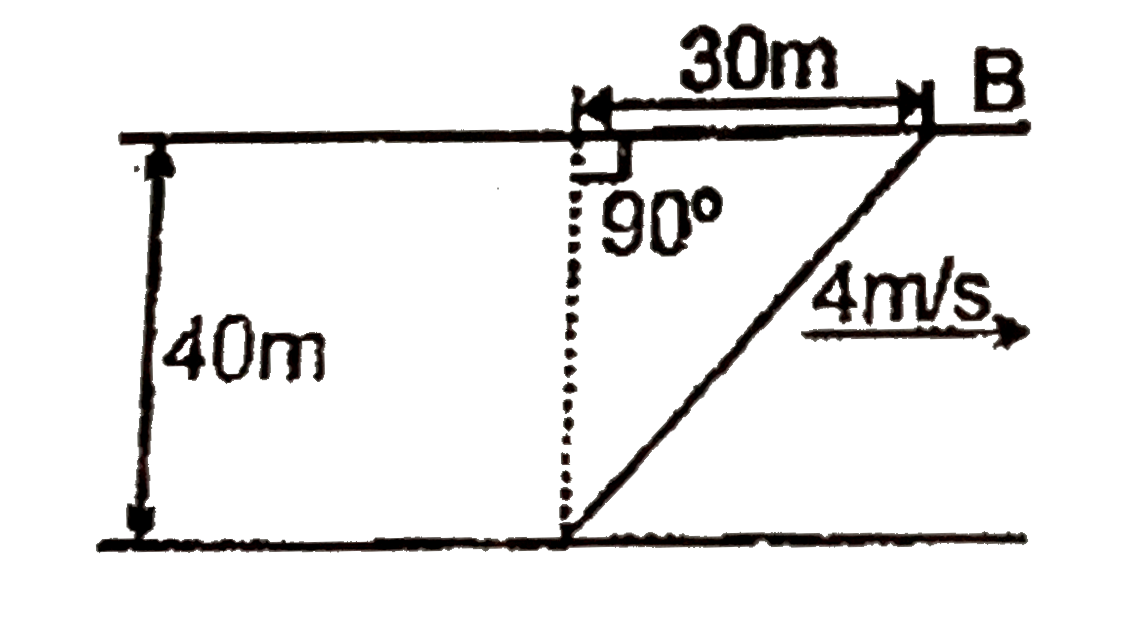
8m/s
3.2m/s
6.5m/s
7√2m/s
The correct Answer is:B
Note that speed of swimmer and angle both are unknown we have to determine function of speed and maximize it. Time taken for x-component of y-component of displacement are same.
→vS/R=ucosθˆi+usinθˆj
→VR/E=υˆi
→VS/E=(ucosθ+υ)ˆi+usinθˆj
θ0ucosθ+υ=40usinθ
⇒3usinθ=4ucosθ+16
⇒3usinθ−4ucosθ=16
⇒u=163sinθ−4cosθ
for Umin,f(θ)=3sinθ−4cosθshould be maximum
f(θ)max=5
Umin=165m/s
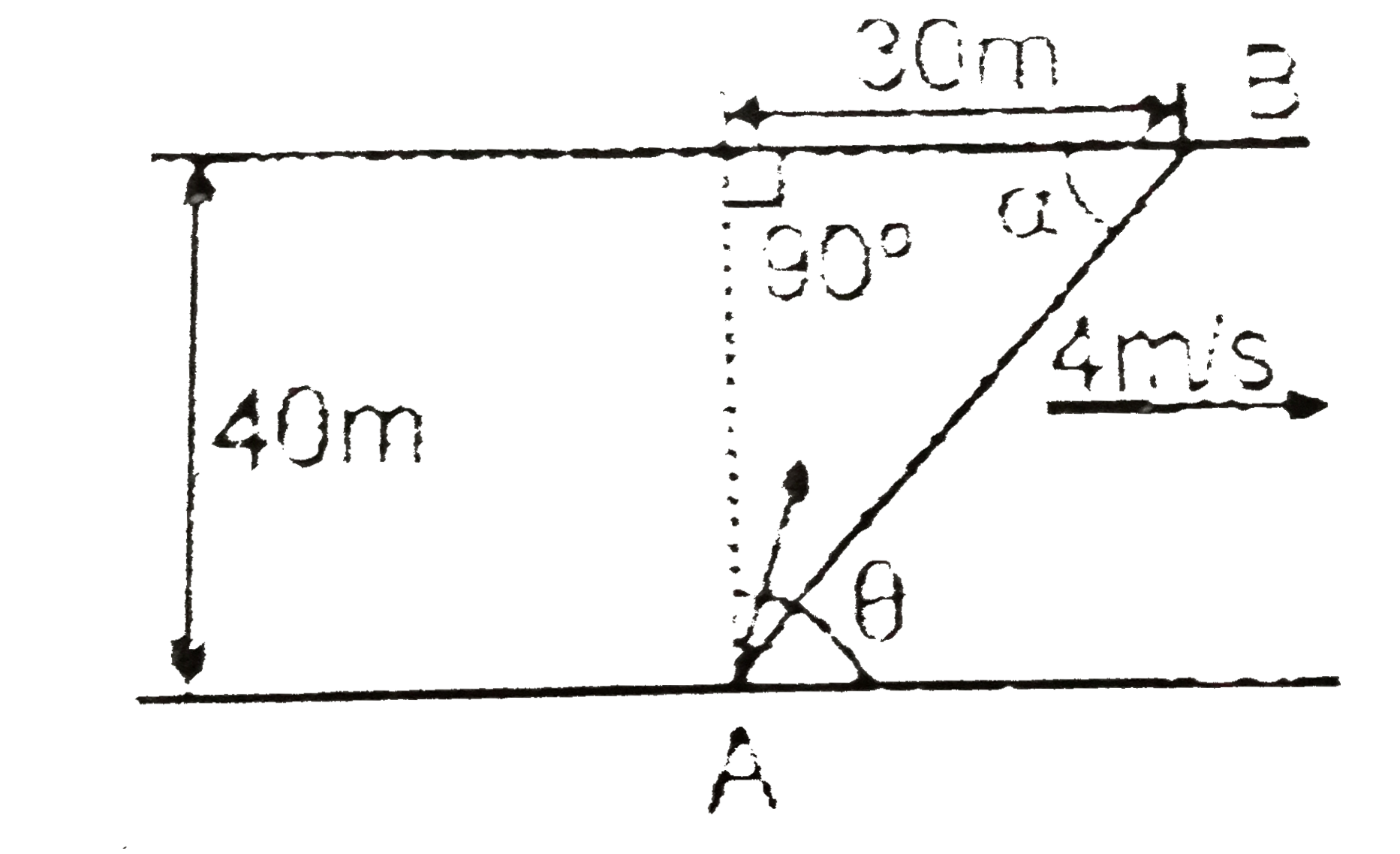
Topper's Solved these Questions
Similar Questions
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the fig 1E.125 (a) what minimum speed relative to water should the man have so that he can reach point B directly by swimming? In which direction should he swin?
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
View Solution
Knowledge Check
A man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bA man who can swim at a velocity v relative to water wants to cross a river of width b, flowing with a speed u.
AThe minimum time in which he can cross the river is bvBHe can reach a point exactly opposite on the bank in time t=b√v2−u2ifv>uCHe cannot reach a point exactly opposite on the bank if u>vDHe cannot reach a point exactly opposite on the bank if v>uA person, reaches a point directly opposite on the other bank of a flowing river, while swimming at a speed of 5 m/s at an angle of 120∘ with the flow. The speed of the flow must be
A2.5 m/sB3 m/sC4 m/sD1.5 m/s
A man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
 .
.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionIf you are on the west bank of a river that is flowing north with a speed 4m/s. Your swimming speed relative to the water is 5 m/s, and the river is 60m wide. What is your path relative to earth that allows you to cross the river in the shortest time? Explain your reasoning.
View Solution(a) In which direction should the motorboat given in Illustration 5.46 head in order to reach a point on the opposite bank directly east from the starting point ? The boat's speed relative to the water remains 4ms−1.
(b) What is the velocity of the boat relative to the earth ?
( c) How much time is required to cross the river ?
View SolutionA man can swin with speed 6 km/h in still water. If he tries of swim across a river flowing with speed 5km/h, how fast does a leaf floating on water appears to go , to the man ?
View Solution

