A man wants to reach point B on the opposite bank of a river flowing at a speed as shown in figure. What minimum speed relative to water should the man have so that he can reach point B? In which direction should he swim?
The correct Answer is:B
To solve the problem of a man wanting to reach point B on the opposite bank of a river flowing at a certain speed, we can break down the solution into several steps.
1. Understanding the Problem:
- The man is swimming across a river that has a current. We need to determine the minimum speed he must swim relative to the water to reach point B directly across from his starting point.
2. Define Variables:
- Let V be the speed of the river (current).
- Let U be the speed of the man relative to the water.
- The man needs to swim at an angle θ to counteract the current.
3. Break Down the Velocities:
- The man's velocity can be broken down into two components:
- Ucosθ (horizontal component, against the current)
- Usinθ (vertical component, across the river)
4. Set Up the Equation:
- To reach point B directly, the horizontal component of the man's velocity must equal the speed of the river:
Ucosθ=V
- The vertical component must allow him to swim across the width of the river:
Usinθ=Width of the river/t
- Here, t is the time taken to cross the river.
5. Relate Time to Velocity:
- The time t it takes to cross the river can be expressed as:
t=Width of the riverUsinθ
6. Combine the Equations:
- From the first equation, we can express U:
U=Vcosθ
- Substitute this into the second equation:
Vcosθsinθ=Width of the river/t
- Rearranging gives:
t=Width of the rivercosθVsinθ
7. Minimize the Speed:
- To find the minimum speed U, we need to maximize sinθ+cosθ. The maximum value occurs when θ=45∘:
sin45∘=cos45∘=1√2
- Therefore, the minimum speed U can be expressed as:
U=Vcos45∘=V√2
8. Conclusion:
- The minimum speed relative to water that the man should have to reach point B is U=V√2.
- The direction in which he should swim is at an angle of 45∘ to the bank of the river.
Final Answer:
- Minimum speed U=V√2
- Direction: 45∘ to the bank of the river.
- The man is swimming across a river that has a current. We need to determine the minimum speed he must swim relative to the water to reach point B directly across from his starting point.
- Let V be the speed of the river (current).
- Let U be the speed of the man relative to the water.
- The man needs to swim at an angle θ to counteract the current.
- The man's velocity can be broken down into two components:
- Ucosθ (horizontal component, against the current)
- Usinθ (vertical component, across the river)
- To reach point B directly, the horizontal component of the man's velocity must equal the speed of the river:
Ucosθ=V
- The vertical component must allow him to swim across the width of the river:
Usinθ=Width of the river/t
- Here, t is the time taken to cross the river.
- The time t it takes to cross the river can be expressed as:
t=Width of the riverUsinθ
- From the first equation, we can express U:
U=Vcosθ
- Substitute this into the second equation:
Vcosθsinθ=Width of the river/t
- Rearranging gives:
t=Width of the rivercosθVsinθ
- To find the minimum speed U, we need to maximize sinθ+cosθ. The maximum value occurs when θ=45∘:
sin45∘=cos45∘=1√2
- Therefore, the minimum speed U can be expressed as:
U=Vcos45∘=V√2
- The minimum speed relative to water that the man should have to reach point B is U=V√2.
- The direction in which he should swim is at an angle of 45∘ to the bank of the river.
- Minimum speed U=V√2
- Direction: 45∘ to the bank of the river.
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Exercise 6.1
Explore 2 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Exercise 6.2
Explore 3 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Example Type 7
Explore 1 Video
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the fig 1E.125 (a) what minimum speed relative to water should the man have so that he can reach point B directly by swimming? In which direction should he swin?
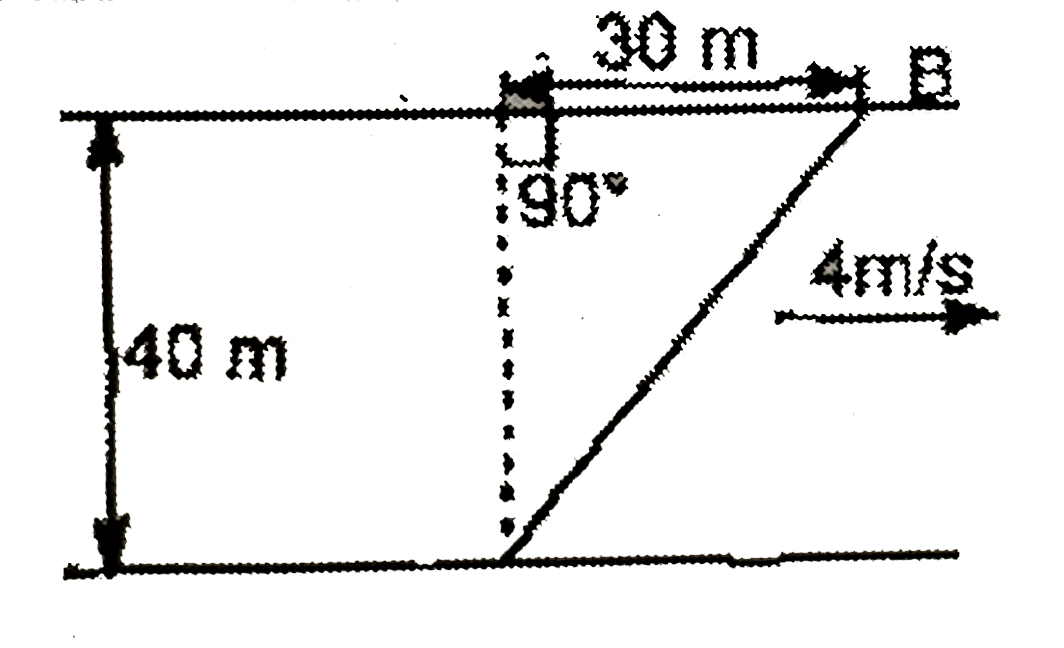
View SolutionA man wants to reach point B on the opposite bank of a river flowing at a speed u as shown in (Fig. 5.193). What minimum speed relative to water to water should the man have so that he can reach directly to point B ? In which direction should he swim ?
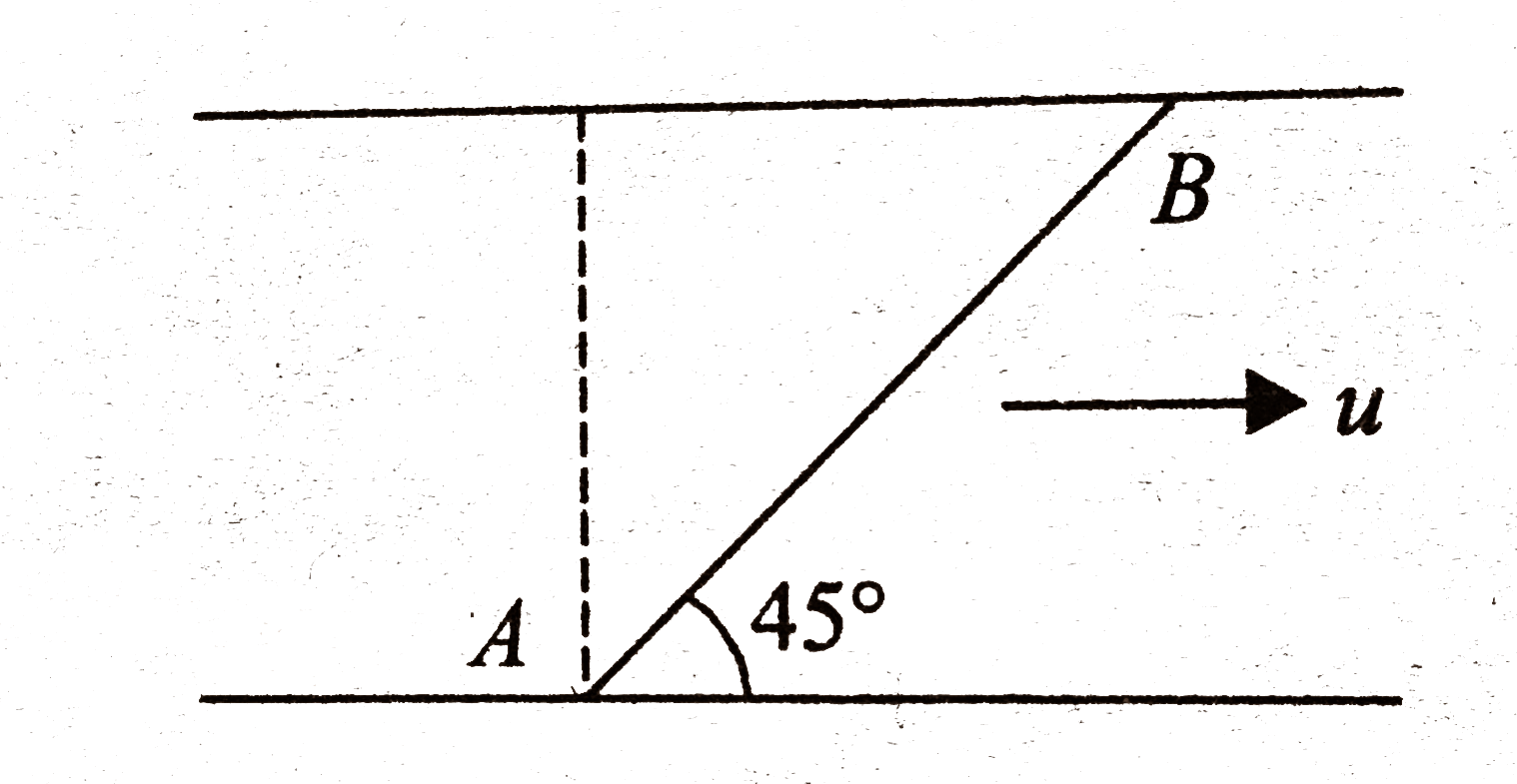 .
.
View Solution
Knowledge Check
A man wants to reach point B on the opposite bank of a river flowing at a speed 4m/s as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B directly by swimming?
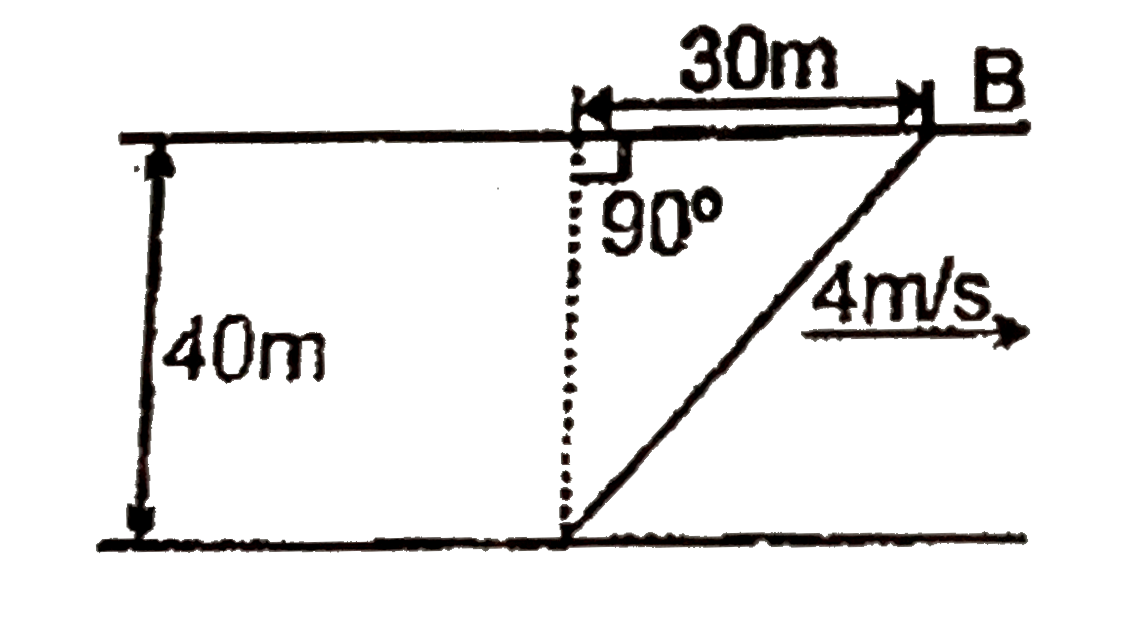 A8m/sB3.2m/sC6.5m/sD7√2m/s
A8m/sB3.2m/sC6.5m/sD7√2m/sA man in a row boat must get from point A to point B on the opposite bank of the river (see figure).The distance BC=a.The width of the river AC=b.At what minimum speed u relative to the still water should the boat travel to reach the point B?The velocity of flow of the river is v0
 Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2b
Av0b√a2+b2Bv0a√a2+b2Cv0b√2aDv0a√2bIf a man wants to hit a target, he should point his rifle-
Ahigher than the targetBlower than the targetCin the direction of the targetDnothing can be said
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?
View SolutionA man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .
.
View SolutionA man can swim in still water with a speed of 2ms−1. If he wants to cross a river of water current speed √3ms−1 along the shortest possible path, then in which direction should he swim ?
View Solution

