The mass M shown in the figure oscillates in simple harmnonic motion and amplitude A. The amplitude of the point P is
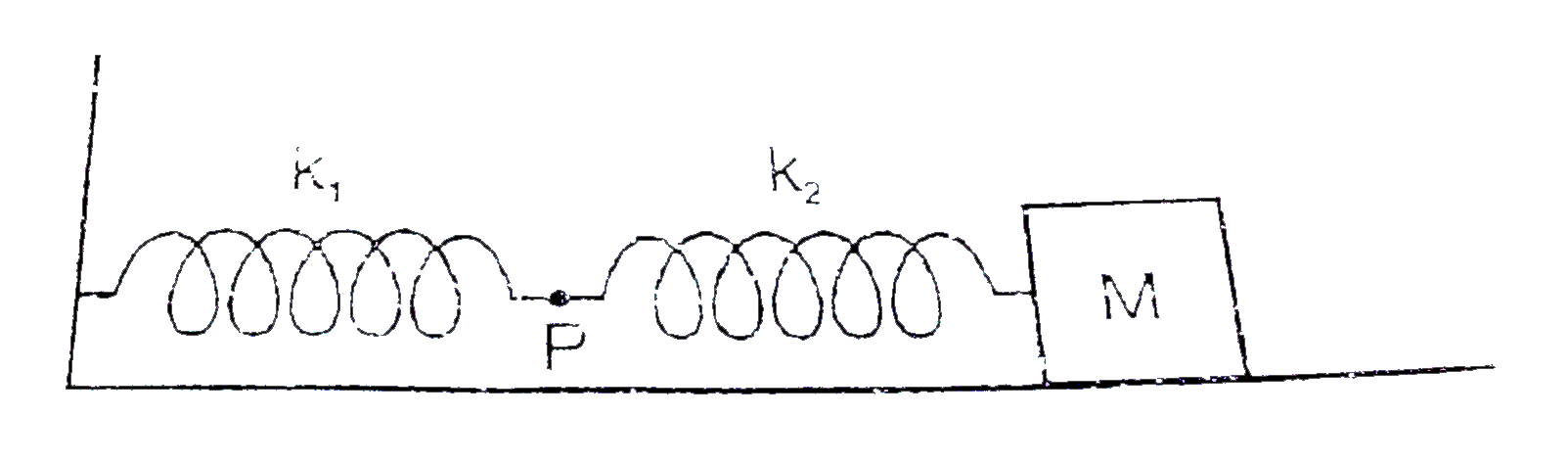
k1Ak2
k2Ak1
k1Ak1+k2
k2Ak1+k2
The correct Answer is:D
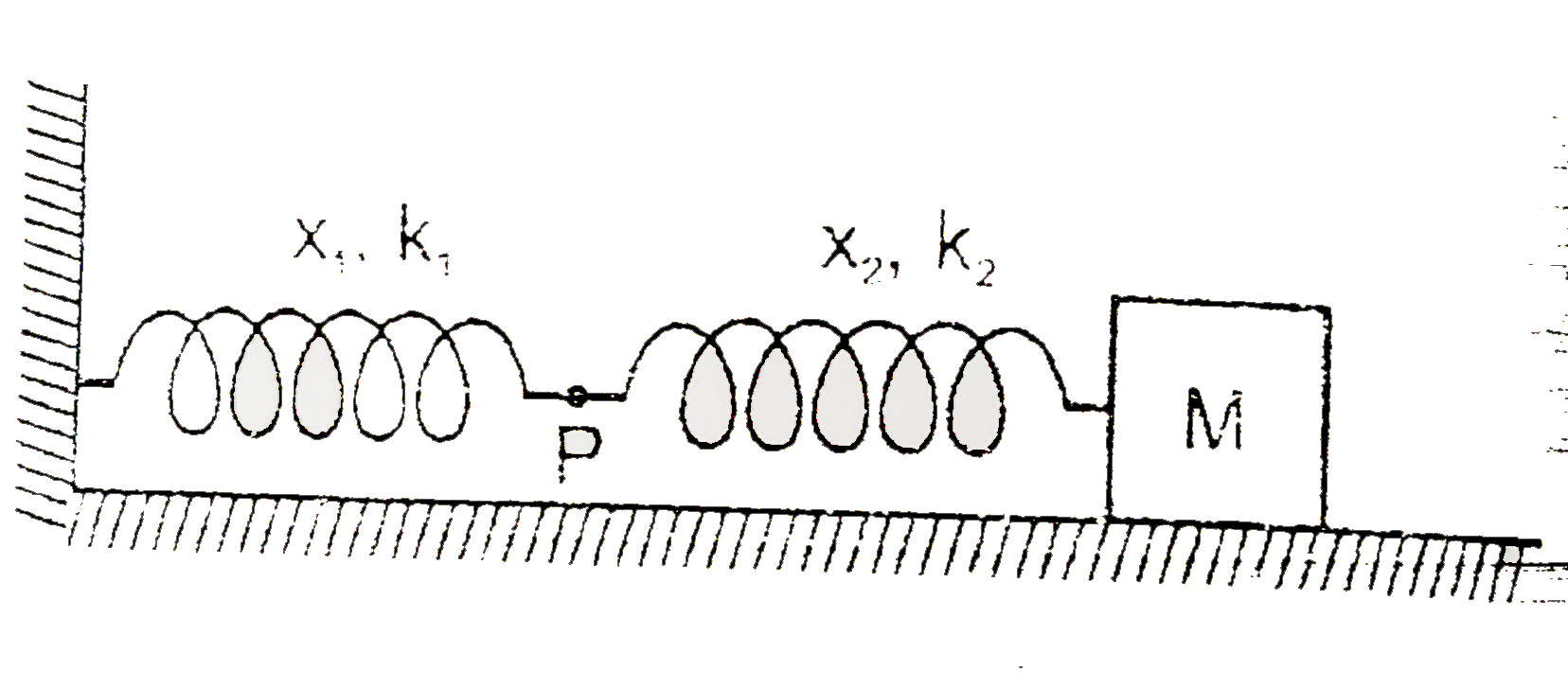
Extensions in springs are x1 and x2 then
k1x1=k2x2
and x1+x2=A
⇒x1+k1x1k2=A⇒x1=k2Ak1+k2
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II
17 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV
8 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
The figure shows a mass M attached to a series arrangement of two springs of spring constants k1andk2 where k2=2k1. If the mass M oscillates in simple harmonic motion with amplitude A, the amplitude of the point O is αAβ. Find β−α.

View SolutionA particle executes simple harmonic motion of amplitude A. At what points is its speed half the maximum speed ?
View Solution
Knowledge Check
The mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
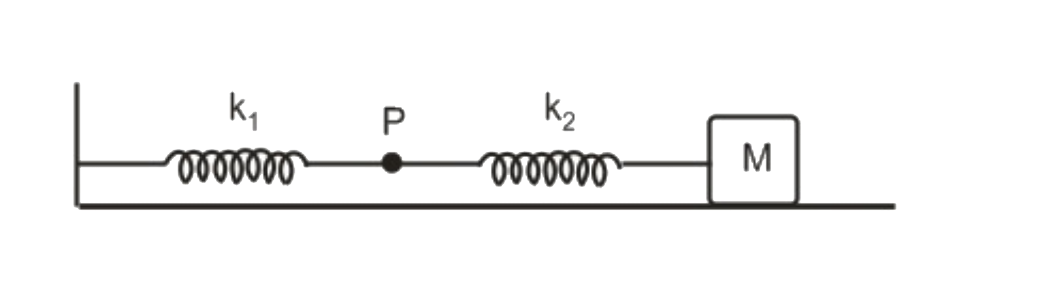 Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1
Ak1Ak2Bk2Ak2−k1Ck2Ak1+k2Dk2Ak1The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The maximum speed of junction P is V0. Assume springs are massless. Select the correct option/s
 AAmplitude of potential energy is springs S1 and S2 is respectivley 19kA2 and kA2BAmplitude of potential energy is S1 and S2 is respectively 29kA2 and 19kA2CV0=A√8k27MDV0=A√8k81M
AAmplitude of potential energy is springs S1 and S2 is respectivley 19kA2 and kA2BAmplitude of potential energy is S1 and S2 is respectively 29kA2 and 19kA2CV0=A√8k27MDV0=A√8k81MThe total work done by the restoring force in simple harmonic motion of amplitude A and angular velocity ω in one oscillation is
A12mω2A2BmA2ω2CZeroD12mAω
A simple harmonic motion is represented by F(t)=10sin(20t+0.5). The amplitude of the S.H.M. is
View SolutionThe maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
View SolutionA mass m oscillates with simple harmonic motion with frequency f=ω2π and amplitude A on a spring of stiffness constant K. Which of the following is not correct ?
View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?

View SolutionThe total work done by a restoring force in simple harmonic motion of amplitude A and angular velocity. ω, in one oscillation is
View Solution
