A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.

The maximum value of V0 for whic the disk will roll without slipping is-
μg√Mk
μg√M2k
μg√3Mk
μg√5M2k
The correct Answer is:C
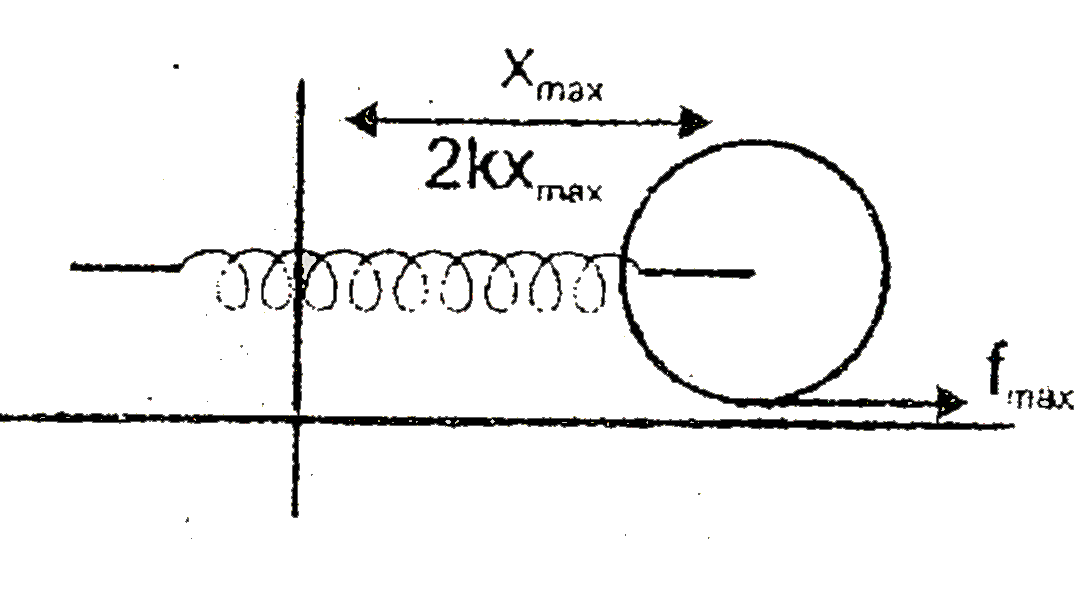
12MV02+12MR22(V0R)2=12(2K)x2max
=32MV02=2kx2max⇒xmax=√34Mv02K
At extreme position, frication will have maximum value.
2kxmx−fmax=4k3xmax⇒fmax=23kxmx
μMg=23=23k√34Mv02K⇒μMg=(√K3M)V0
V0=μMG√3MK
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II
17 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - IV
8 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View Solution
Knowledge Check
A uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
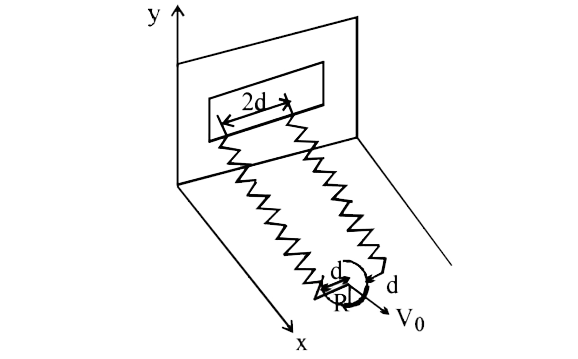
The centre of mass of the disk undergoes simple harmonic motion with angular frequency ω equal to -A√kMB√2MC√2k3MD√4k3MA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
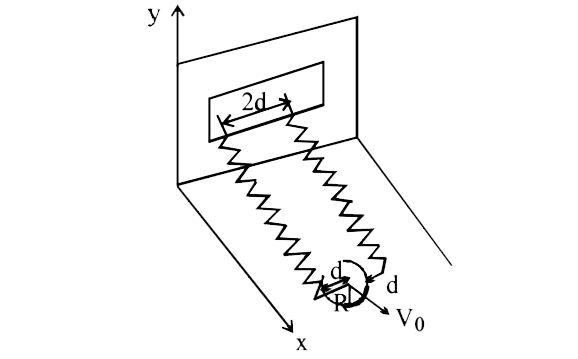
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.A=−kxB−2kxC−2kx/sD−4kx/3A particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mk
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA body of mass 0.4 kg is held between two massless springs whose ends are fixed to rigid walls as shown in the figure. The spring constants are 8 N/m and 2 N/m. If the body is displaced along the direction of the lengths of the springs and released, the time period (in second) of the oscillations will be (ignore vertical oscillation, if any )

View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

View SolutionTwo identical massless springs A and B consist spring constant kA and kB respectively. Then :
View SolutionA bob of mass m is connected to a spring of spring constant k and a string which is fixed to the ceiling as shown in figure. Original length of the spring is L and the bob rotates in a horizontal circle centred at the fixed rod. Assuming the spring remains horizontal, then elongation in the spring is :

View Solution
