A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find the minimum distance of the particle from B during the motion.
a6
a4
a3
a8
The correct Answer is:A
(i) force on particle at point P
f=2mg(a−x)a−mg(x)a
F=mga(2a−3x)
m F=−3mga(x−2a/3)
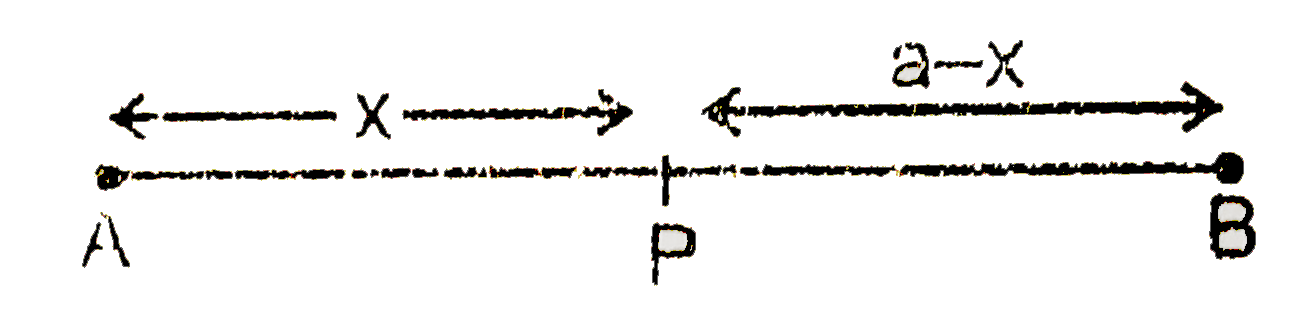
(ii) So this is equation of S.H.M.(F=mω2x) so particle
Perform S.H.M. with mean position x−2a/3=0
So ω2=3ga⇒ω=√3g/a
So Time period T=2π√a/3g
and amplitude =2a/3−a/2=a/6
(iii) minimum distance from B
=a−(2a/3+a/6)=a/6
(iv) at point P velocity of partivle =0
and force =2mgxa
(at point q)
acc. =2gxa⇒v∫ovdv=a/6∫o2gxdxa⇒V=√2ga6

Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - I
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II
17 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III
12 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
A particle of mass 4kg moves between two points A and B on a smooth horizontal surface under the aciton of two forces such that when it is at a point P, the forces are 2→PAN and 2→PBN. If the particle is released from rest at A, find the time it takes to travel a quarter of the way A to B.
View SolutionTwo strange particles A and B in space, exert no force on each other when they are at a separation greater than x0=1.0 m. When they are at a distance less than x0, they repel one another along the line joining them. The repulsion force is constant and does not depend on the distance between the particles. This repulsive force produces an acceleration of 6ms–2 in A and 2ms–2 in B when the particles are at separation less than x0. In one experiment particle B is projected towards A with a velocity of 2ms–1 from a large distance so as to hit A head on. The particle A is originally at rest and the system of two particles do not experience any external force.
(a) Find the ratio of mass of A to that of B.
(b) Find the minimum distance between the particles during subsequent motion. (c) Find the final velocity of the two particles.
View Solution
Knowledge Check
A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.A√2ga3B√2ga6C√2ga5D√ga3A particle of mass 'm' moves on a horizont smooth line AB of length 'a' such that when particle is at any general point P on the line two force act on it. A force mg(AP)a towards A and another force 2mg(BP)a towards B.
Find its time period when released from rest from mid-point of line AB.AT=2π√3agBT=2π√a2gCT=2π√agDT=2π√a3gA particle of mass m moves along a circle of 'R'. The modulus of the average vector of force acting on the particle over the distance equal to a quarter of the circle is :
Azero if the particle moves with uniform speed vB√2mv2πR if the particle moves with uniform speed vC√2mv2πR if the particle moves with uniform speed vDma if particle moves with constant tangential acceleration 'a', the initial velocity being equal to zero
A particle of mass m moves with constant speed v on a circular path of radius r as shown in figure. The average force on it during its motion from A to B is

View SolutionA charge "Q" of mass "m" is at rest on a smooth horizontal plane.Another identical particle is projected with a velocity v towards it from long distance then
View SolutionA particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionTo keep a particle moving with constant velocity on a frictionless surface, an external force .
View Solution