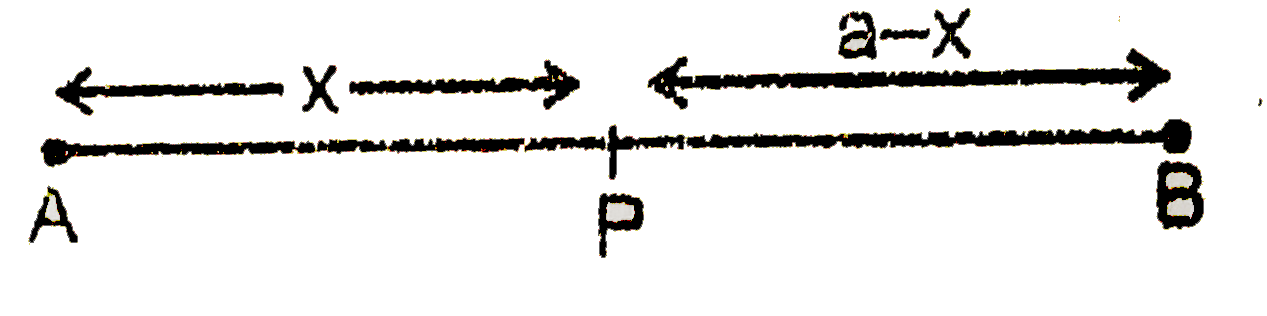
A particle of mass $' m'$ moves on a horizont smooth line $A B$ of length $' a'$ such that when particle is at any general point $P$ on the line two force act on it. A force $\frac{m g (A P)}{a}$ towards $A$ and another force $2 \frac{m g (B P)}{a}$ towards $B$ .
Find its time period when released from rest from mid-point of line $A B$ .

A

$T = 2 π \sqrt{\frac{3 a}{g}}$

B

$T = 2 π \sqrt{\frac{a}{2 g}}$

C

$T = 2 π \sqrt{\frac{a}{g}}$

D

$T = 2 π \sqrt{\frac{a}{3 g}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$(i)$ force on particle at point $P$
$f = \frac{2 m g (a - x)}{a} - \frac{m g (x)}{a}$
$F = \frac{m g}{a} (2 a - 3 x)$
m $F = \frac{- 3 m g}{a} (x - 2 a / 3)$

$(i i)$ So this is equation of $S . H . M . (F = m ω^{2} x)$ so particle
Perform $S . H . M .$ with mean position $x - 2 a / 3 = 0$
So $ω^{2} = \frac{3 g}{a} \Rightarrow ω = \sqrt{3 g / a}$
So Time period $T = 2 π \sqrt{a / 3 g}$
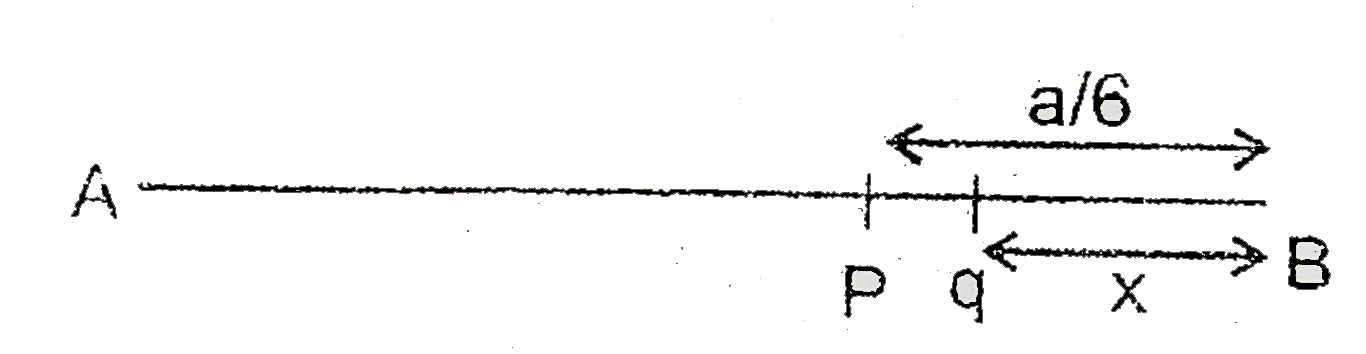
and amplitude $= 2 a / 3 - a / 2 = a / 6$
$(i i i)$ minimum distance from $B$
$= a - (2 a / 3 + a / 6) = a / 6$
$(i v)$ at point $P$ velocity of partivle $= 0$
and force $= \frac{2 m g x}{a}$
(at point $q$ )
acc. $= \frac{2 g x}{a} \Rightarrow v \int o v d v = a / 6 \int o \frac{2 g x d x}{a} \Rightarrow V = \frac{\sqrt{2 g a}}{6}$

|

Updated on:21/07/2023

Class 12 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass $' m'$ moves on a horizont smooth line $A B$ of length $' a'$ such that when particle is at any general point $P$ on the line two force act on it. A force $\frac{m g (A P)}{a}$ towards $A$ and another force $\frac{2 m g (B P)}{a}$ towards $B$ .
Find the minimum distance of the particle from $B$ during the motion.
A $\frac{a}{6}$
B $\frac{a}{4}$
C $\frac{a}{3}$
D $\frac{a}{8}$
Question 2 - Select One
A particle of mass $' m'$ moves on a horizont smooth line $A B$ of length $' a'$ such that when particle is at any general point $P$ on the line two force act on it. A force $\frac{m g (A P)}{a}$ towards $A$ and another force $\frac{2 m g (B P)}{a}$ towards $B$ .
If the force acting towards A stops acting when the particle is nearest to B then find the velocity with which it crosses point B.
A $\frac{\sqrt{2 g a}}{3}$
B $\frac{\sqrt{2 g a}}{6}$
C $\frac{\sqrt{2 g a}}{5}$
D $\frac{\sqrt{g a}}{3}$
Question 3 - Select One
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as $F = K / V$ K is constant then speed of the particle in time t
A $\sqrt{\frac{k t}{m}}$
B $\sqrt{\frac{2 k t}{m}}$
C $2 \sqrt{\frac{k t}{m}}$
Dnone of these

RESONANCE-SIMPLE HARMONIC MOTION -Exercise- 2, PART - IV

Home
Ask Doubt
Profile