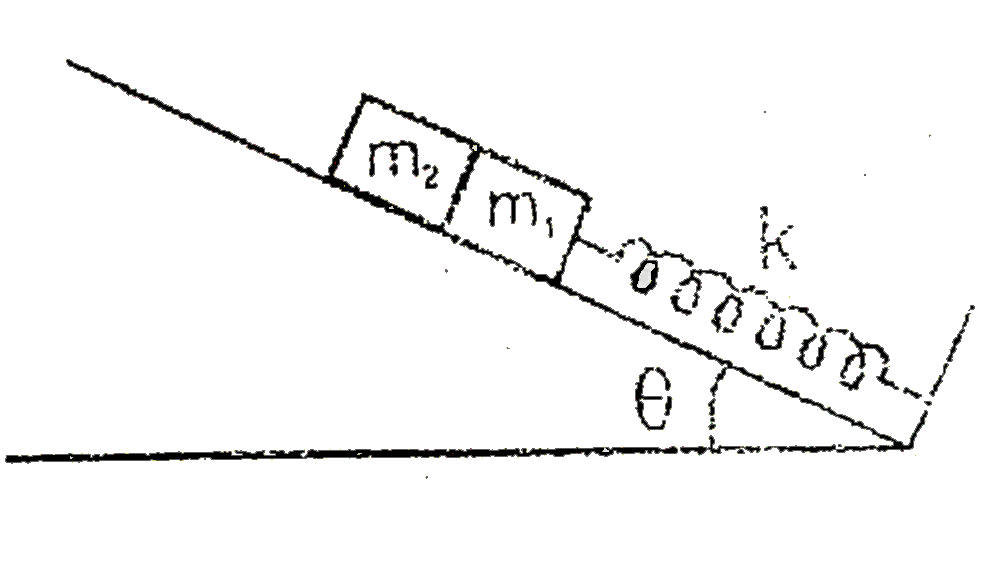
Spring of spring constant k is attached with a block of mass m1, as shown in figure. Another block of mass m2 is placed angainst m1, and both mass masses lie on smooth incline plane.

Find the compression in the spring when lthe system is in equilibrium.
(√13k(m1+m2))gsinθ
(√2k(m1+m2))gsinθ
(√3k(m1+m2))gsinθ
(√1k(m1+m2))gsinθ
The correct Answer is:C
At equilibrium position : →
Kx0=m1gsinθ+m2gsinθ
x0=(m1+m2)gsinθk
Block will separate when acceleration of block of mass m1 will be just equal to gsinθ
⇒a=ω2x=gsinθ
⇒Km1+m2×x=gsinθ
x=m1+m2Kgsinθ=x0
So, blocks will separate when blocks are at distance x=m1+m2Kgsinθ
From mean position
i.e. spring is at its natural position (amplitude A=(2K(m1+m2)gsinθ'))
Blocks will seoparte at distance x=x0 from mean position.
v=√A2−x20
=√Km1+m2√(2K(m1+m2)gsinθ)2−((m1+m2K)gsinθ)2
=√3k(m1+m2)gsinθ
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - I
20 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 3, PART - II
17 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III
12 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View Solution
Knowledge Check
A block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
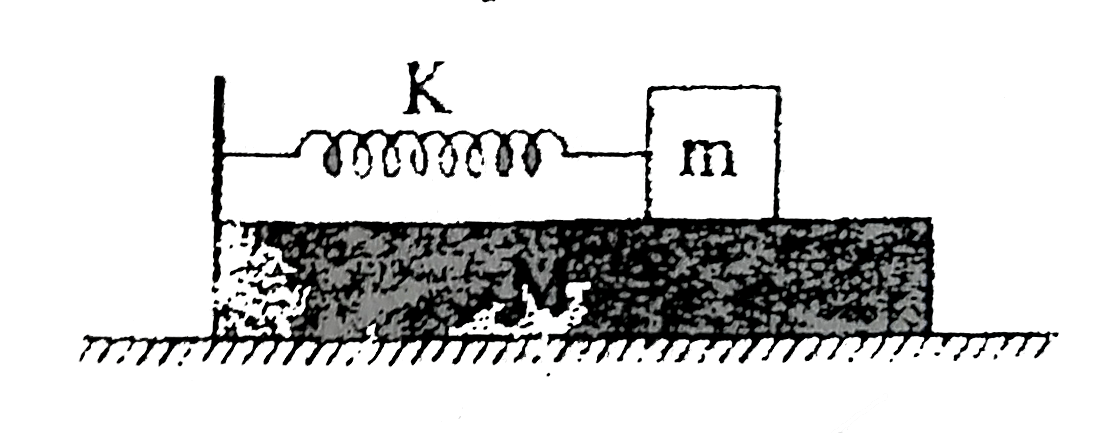 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0Two blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correctA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)
 AThe block will executes SHMBAmplitude of oscillation is F2KCTime period of oscillation is 2π√mkDThe maximum speed of block is √2Fx−kx2m (Here, x=F/k).
AThe block will executes SHMBAmplitude of oscillation is F2KCTime period of oscillation is 2π√mkDThe maximum speed of block is √2Fx−kx2m (Here, x=F/k).
Tow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

View SolutionIn the fig 4.24 a block of mass m moves with velocity v0 toward a stationaly block of a mass M on a smooth horizontal surface. Find the maximum compression in the spring of stiffnesss constant K.

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

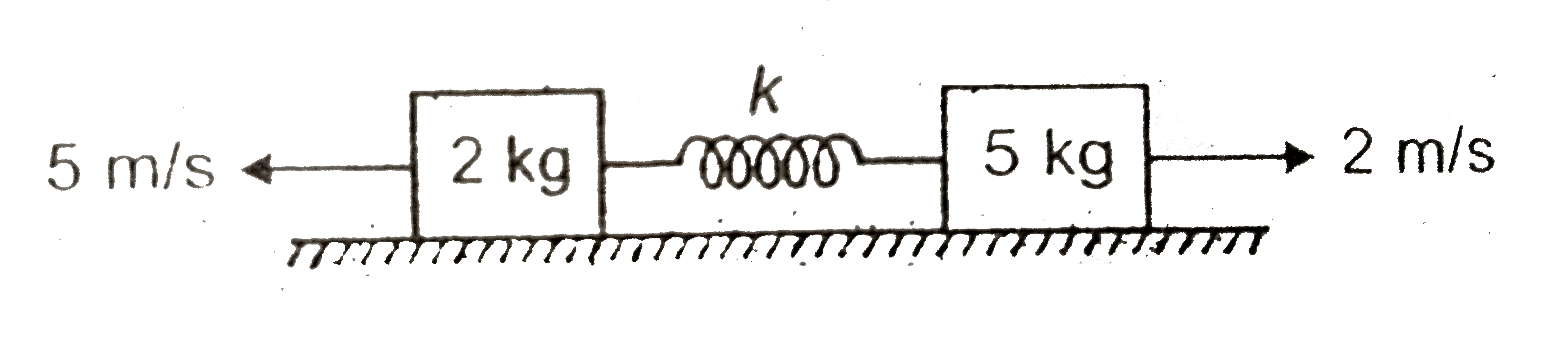
View SolutionTwo blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
View Solution
