A box is placed on a smototh plane end it is free to move. A single penldulum is attached in the block. Find its time period.

Let Fp= Pseudo force
For equilibrium position
Tsinα+FP=mgsinθ
Tsinα+ma=mgsinθ
since a=gsinθ
Tsinα+mgsinθ=mgsinθ
Tsinα=0
∴α=0
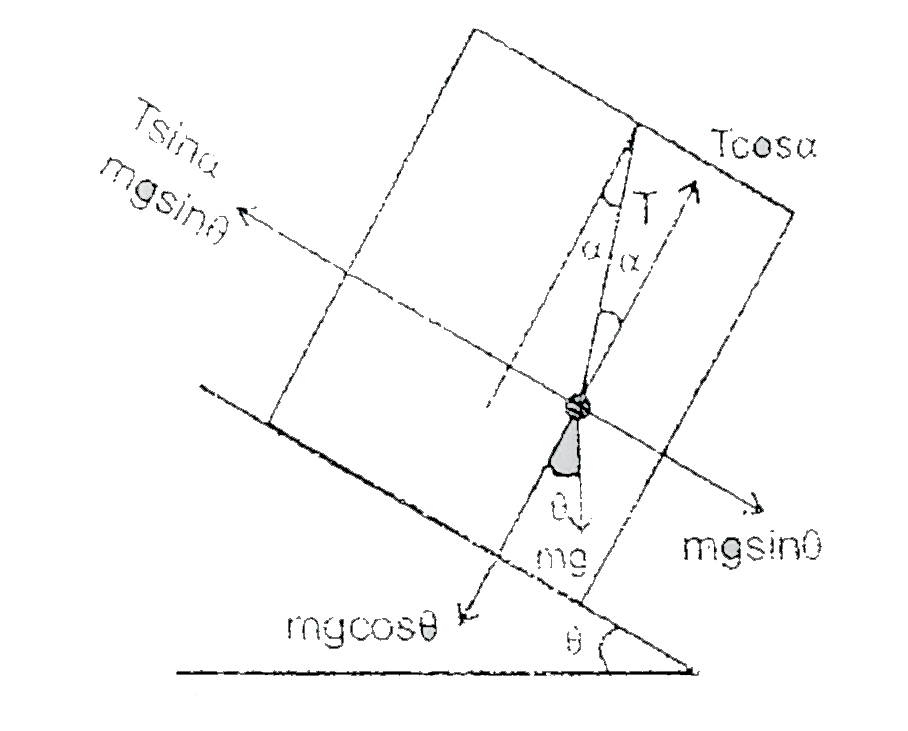
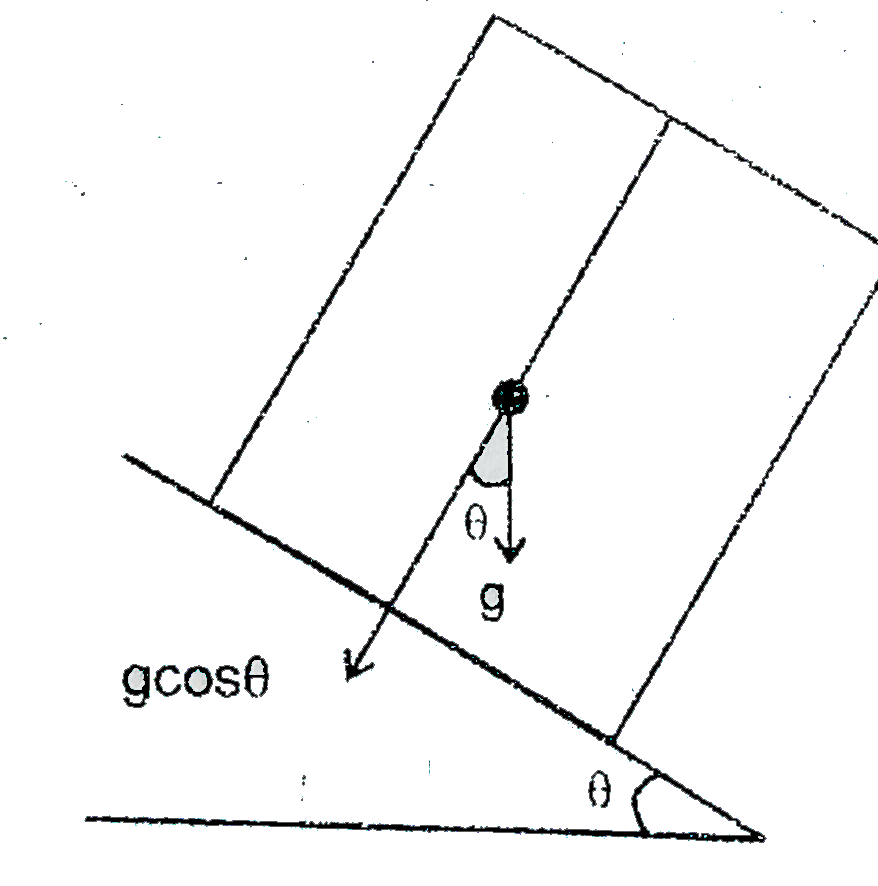
Hence in equilibrium position the string is perpendicular to incline plane.
Therefore effective 'g' is
geff=gcosθ
Time period
T=2π√lgeff
T=2π√lgcosθ Ans.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise
24 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- SEMICONDUCTORSBOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-3
30 Videos
Similar Questions
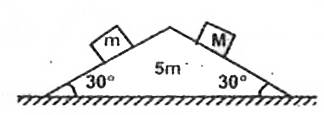
Two blocks of masses M and m are held on a smooth wedge. The wedge is placed on smooth plane and is free to move on plane. Now both blocks are released, and it is found that block m remains stationary w.r.t. the wedge, the ratio of M/m is 6k. Find the value k.
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View Solution
Knowledge Check
A block of mass m is placed on a rough inclined plane. When the inclination of the plane is θ , the block just beging to slide down the plane under its own weight. The minimum force applied parallel to the plane, to move the block up the plane, is.
AmgsinθB2mgsinθCmgcosθDmgtanθA uniform semi circular ring of radius R and mass m is free to oscillate about its one end in its vertical plane as shown in the figure. Find time period of SHM of its centre of mass of the ring (take π2=10)
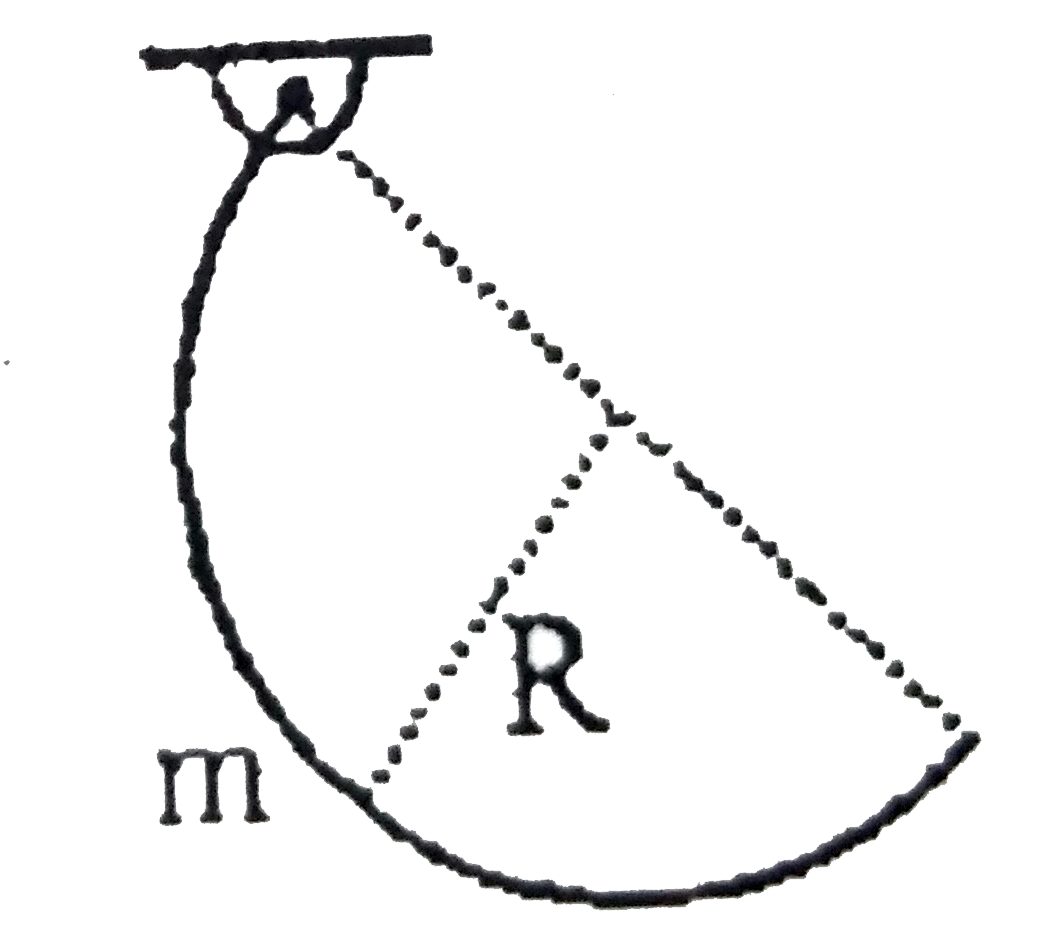 A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)
A2π√RgB2π√Rg(√207)C2π√2RgD2π√Rg(145)A uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)
 AMl1(l2−l1)B2Ml1(l2−l1)CMl12(l2−l1)DM(l1+l2)2l1
AMl1(l2−l1)B2Ml1(l2−l1)CMl12(l2−l1)DM(l1+l2)2l1
A block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
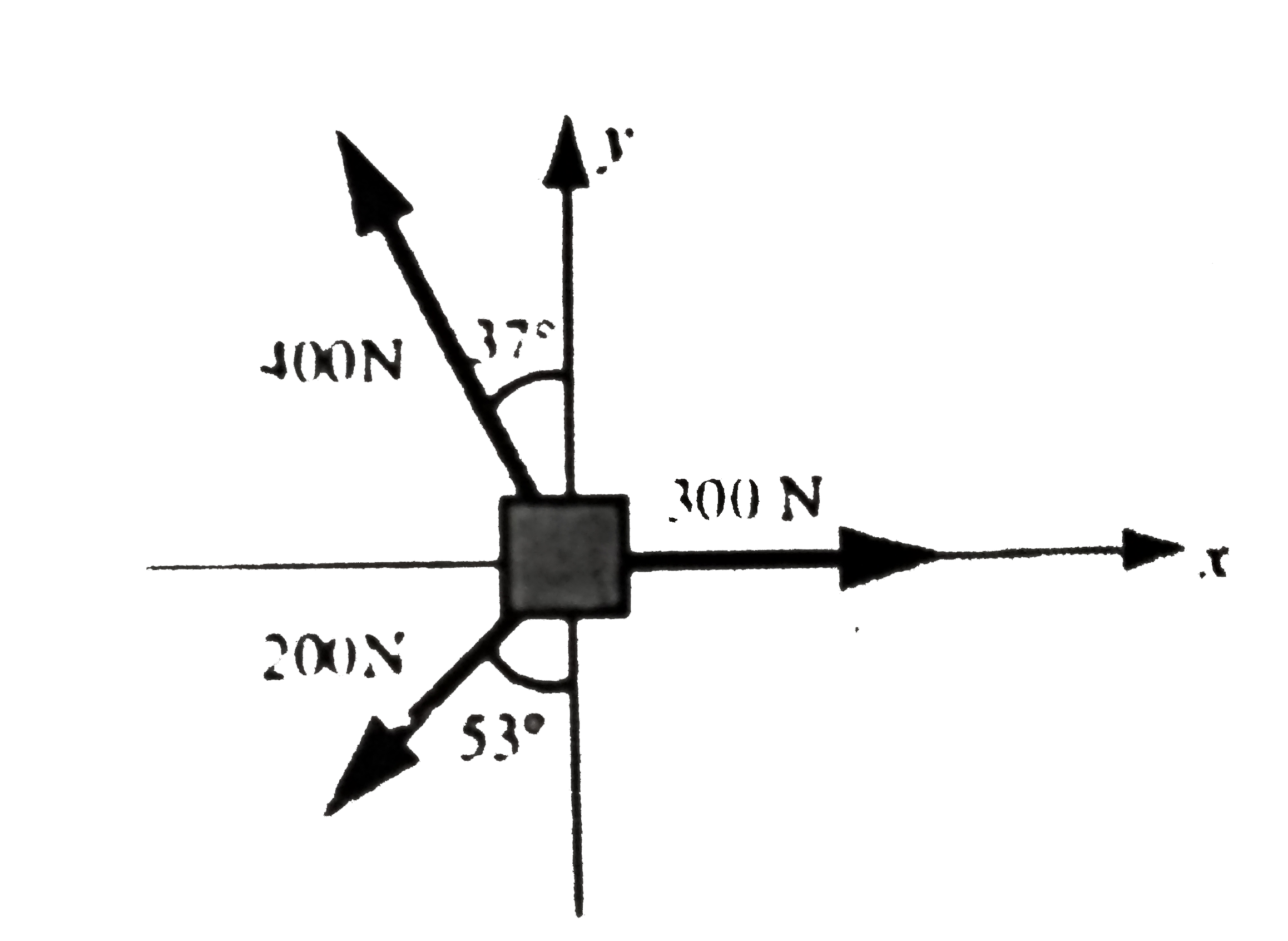
View SolutionBlock A of mass m is performing SHM of amplitude a. Another block B of mas m is gently placed on A when it passes through mean position and B sticks to A. Find the time period and amplitude of new SHM.
View SolutionA block of mass m is attached to a massless spring of force constant k, the other end of which is fixed from the wall of a truck as shown in the figure. The block is placed over a smooth surface and initially the spring is unstretched. Suddenly the truj starts moving towards right with a constant acceleration a0. If the block is observed from the truck

View SolutionThe free and of a simple pendulum is attached to the ceiling of a box. The box is taken to a height and the pendulum is oscillated. When the bob is at its lowest point the box is released to fall freely. As sen from the box during this period the bob will
View SolutionA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
View Solution
