S1 and S2 are two sources of light which produce individually disturbance at point P given by E1=3sinωt,E2=4cosωt. Assume −→E1&→E2 to along the same line, find the resultant after their superposition.
Video Solution
Text Solution
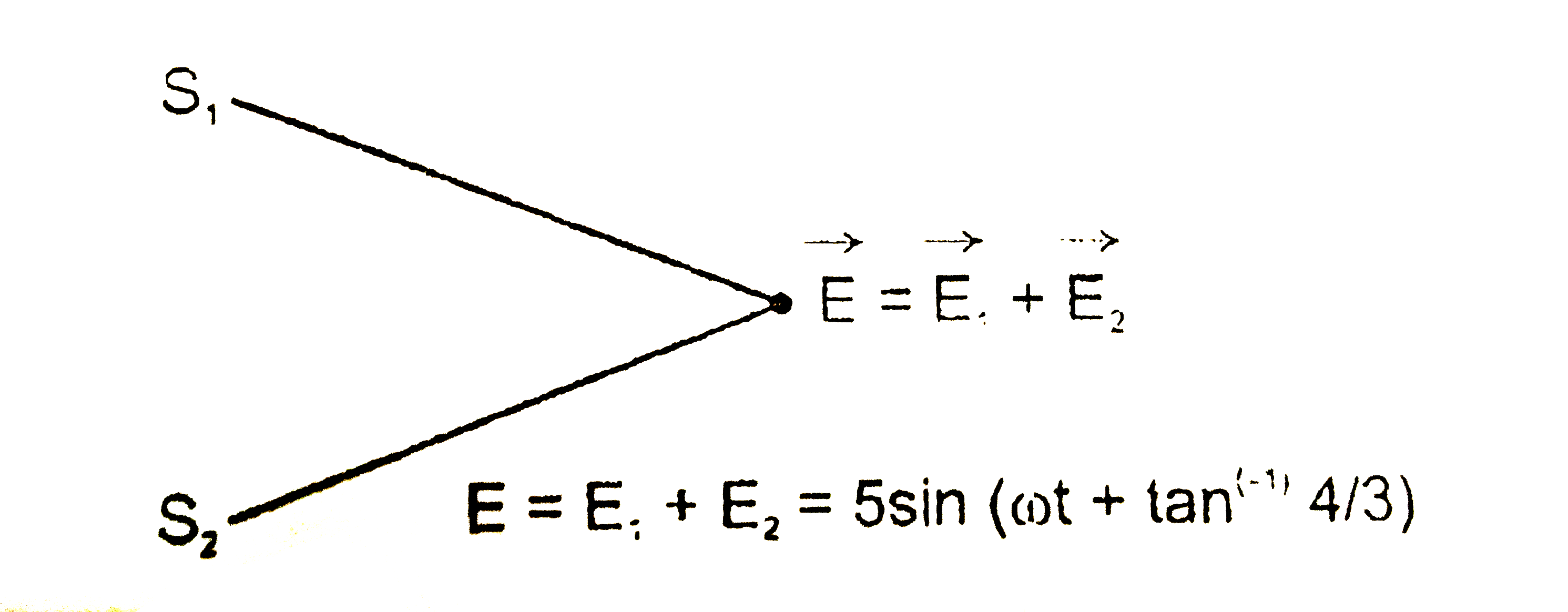
E=3sinωt+4sin(ωt+π2)
A2=32+42+2(3)(4)cos(π)2=52
tanϕ0(4sin)π23+4cos(π2)=43⇒ϕ0=53∘
E=5sin[ωt+53∘]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
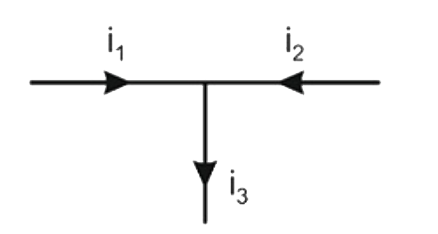
In the given figure, if i1=3sinωtandi2=4cost, then i3 is
 A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5cos(ωt+53∘)
A5sin(ωt+53∘)B5sin(ωt+37∘)C5sin(ωt+45∘)D5cos(ωt+53∘)The displacement of two interfering light waves are given by y1=3sinωt,y2=4sin(ωt+π/2). The amplitude of the resultant wave is
A3B5CzeroDoneTwo waves y1=2sinωt and y2=4sin(ωt+δ) superimpose. The ratio of the maximum to the minimum intensity of the resultant wave is
A9B3CinfinityDZero
x1=5sin(ωt+30∘)
x2=10cos(ωt)
Find amplitude of resultant SHM.
View SolutionTwo waves y1=2sinωt and y2=4sin(ωt+δ) superimpose. The ratio of the maximum to the minimum intensity of the resultant wave is
View Solutionit the two waves represented dy y1=4cosωt and y2=3cos(ωt+π/3) interfere at a point, then the amplitude of the resulting wave will be about
View SolutionTwo waves y1=asin(ωt−kx) and y2=acos(ωt−kx) superimpose at a point :
View SolutionThe light waves from two independent monochromatic light sources are given by, y1=2sinωt and y2=3cosωt. Then the correct statement is
View Solution