_E01_102_Q01.png)
In a YDSE a parallel beam of light of wavelength 6000Å is incident on slits at angle of incidence 30∘. A and B are two thin transparent films each of refractive index 1.5. thickness of A is 20.4μm. Light coming through A and B have intensities I and 4I resepctively on the screen. Intensity at point O which is symmetric relative to the slits is 3I. The central maxima is above O.
(i). what is the maximum thickness of B to do so. Assuming thickness of B to be that found in part (i) answer the following parts.
(ii). Find fringe width, maximum intensity and minimum intensity on screen.
(iii). Dinstance of nearest minima from O
(iv) intensity at 5 cm on either side of O.
The correct Answer is:(a) tB=120μm
(b) β=6mm;Imax=9I,Imax=I
(c) β/6=1mm (d) I(at5 cmaboveO)=9 I<br>I("at" 5 cm "below" O)=3I
(a) For maxima thickness of B. the central maxima is just above O.
⇒ Phase difference at O must be =2π3{∴cosϕ=−12for3Iintensity}.
⇒ Path difference at O=2π3×λ2π=λ3
⇒dsin30∘+(μA−1)×tA−(μB−1)tB=λ/3
get tB=120μm.
(b) Now tB=120μm.
bete=λDd=6000×10−10×10.1×10−3=6mm .
Imax=(√4I+√I)2=9I
Imin=(√4I−√I)2=I
(c) ΔP path difference at 'O'
⇒ΔP=dsinθ+(μA−1)tA−(μB−1)tB
=0.1sin30∘+(1.5−1)×20.4−(1.5−1)×120
ΔP=2×10−7m
∴ydD=ΔP
∴y=DdΔP=10.1×10−3×2×10−7=y=2mm
∴β=λDd=6mm
distance between maxima and minima =β2=3mm
distance of nearest minima from 'O'=β6=1mm
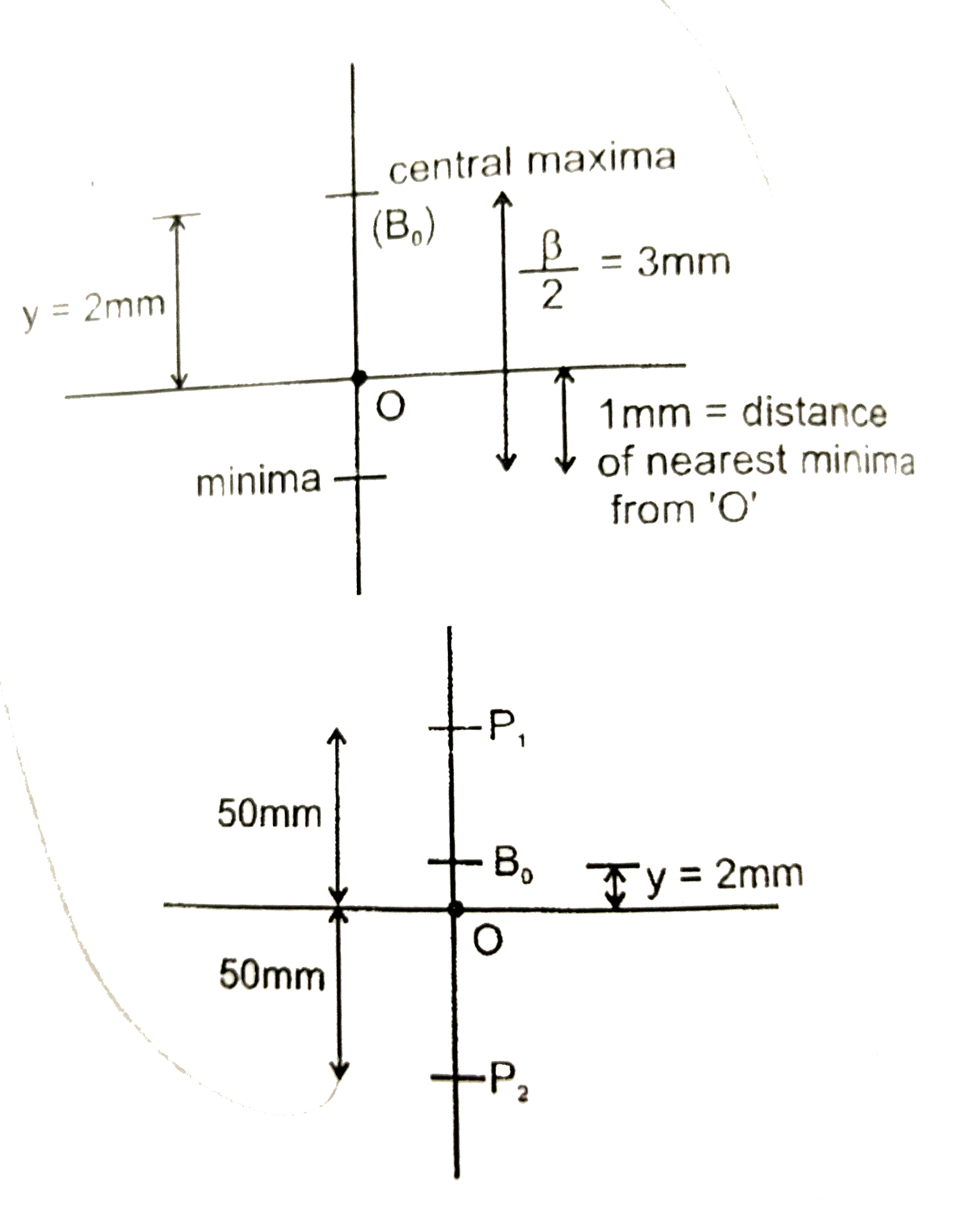
(d) So phase difference at P1
Δϕ=ydD×2πλ
=48×10−3×10−41×2π6000×10−10
Δϕ=16π
Intensity at 'P'1
I1=4I+I+2√4I2cos(16π)
I1=9I
Intensity at point 'P'2
phase differnce at 'P'2
ΔP=2πλ×ΔP
ΔP=ydD=52mm×0.1mm1m
Δϕ=2π6000×10−10×52mm×0.1mm1m
Δϕ=52π3=16π+4π/3
I2=4I+I+2√4I2cos(16π+4π/3)
I2=4I+I+2√4I2cos(4π/3)
=4I+I−2×2I×12
I2=3I
Topper's Solved these Questions
Similar Questions
In YDSE, the central bright fringe produced by light of wavelength 5600Å shifts to the position of 5th bright fringe when a thin transparent film of refractive index 1.28 is introduced in the path of light from one of the two slits. Find the thickness of the film.
View SolutionIn a standard YDSE set up,the intensity at a point where phase difference between the light from the slits is π3 is I0 .The intensity of central maximum will be ?
View Solution
Knowledge Check
Light of wavelength 6000Å is reflected at nearly normal incidence from a soap films of refractive index 1.4 The least thickness of the fringe then will appear black is
AinfinityB200ÅC2000ÅD1000ÅA parallel beam of light of wavelength 6000Å gets diffracted by a single slit of width 0.3 mm. The angular position of the first minima of diffracted light is :
A6×10−3 radB1.8×10−3 radC3×10−3 radD2×10−3 radLight of wavelength 5000Å is incident over a slit of width 1μm. The angular width of central maxima will be
A30∘B60∘C90∘D120∘
The light of wavelength 6328Å is incident on a slit of width 0.2mm perpendicularly, the angular width of central maxima will be
View SolutionA coherent parallel beam of light of wavelength 5000A is incident normally on the plane of slits. The slit S1 is covered with a slab of refractive index μs=1.5 and thickness t=4×10−5m as shown. The separation between the slits is d=1mm and the separtion between the plane of slits and screen is D=1m. Then the position of the central maxima formed on the screen is

View SolutionLight of wavelength 6328Å is incident normally on a slit of width 0.2 mm. Angular width of the central maximum on the screen will be :
View SolutionA parallel beam of sodium light of wavelength 6000Å is incident on a thin glass plate of μ=1.5, such that the angle of refraction in the plate is 60∘. The smallest thickness of the plate which will make it appear dark by reflected light is
View SolutionLight of wavelength 6000Å is normally incident on a slit. Angular position of second minimum from central maximum is 30∘. Width of the slit should be –
View Solution

