Question

A source S is kept directly behind the slit $S_1$ in a double slit apparatus. What will be the phase difference at P, if a liquid of refraction index $\mu$is filled : (wavelength of light in aire is $\lambda$ due to the source, assume $l>>d,D>>d$).

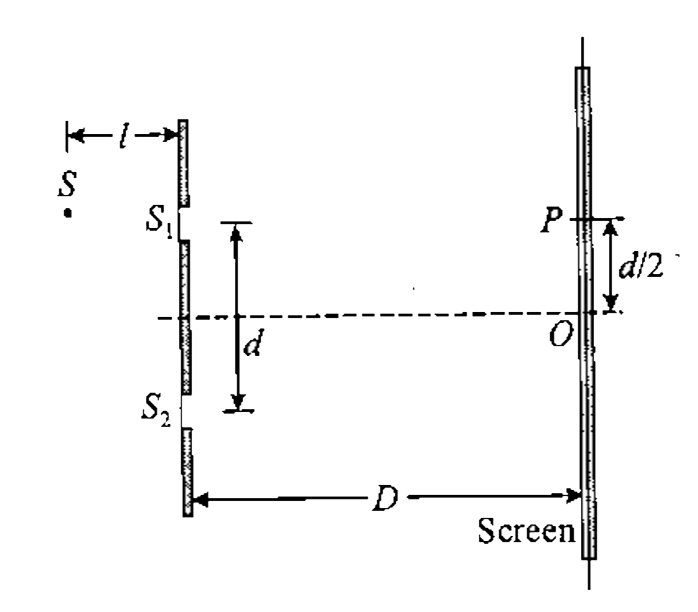
(a) Between the screen and the slits.
(b) Between the slits & the source S. In this case, find the minimum distance between the points on the screen where the intensity is half the maximum intensity on the screen.

Answer

(a) `Deltaphi=((1)/(l)+(mu)/(D)) (pid^(2))/(lambda)`
(b) `Deltaphi=((mu)/(l)+(1)/(D)) (pid^(2))/(lambda)`
`D_(min)=(beta)/(2)=(lambdaD)/(2d)`

Explanation

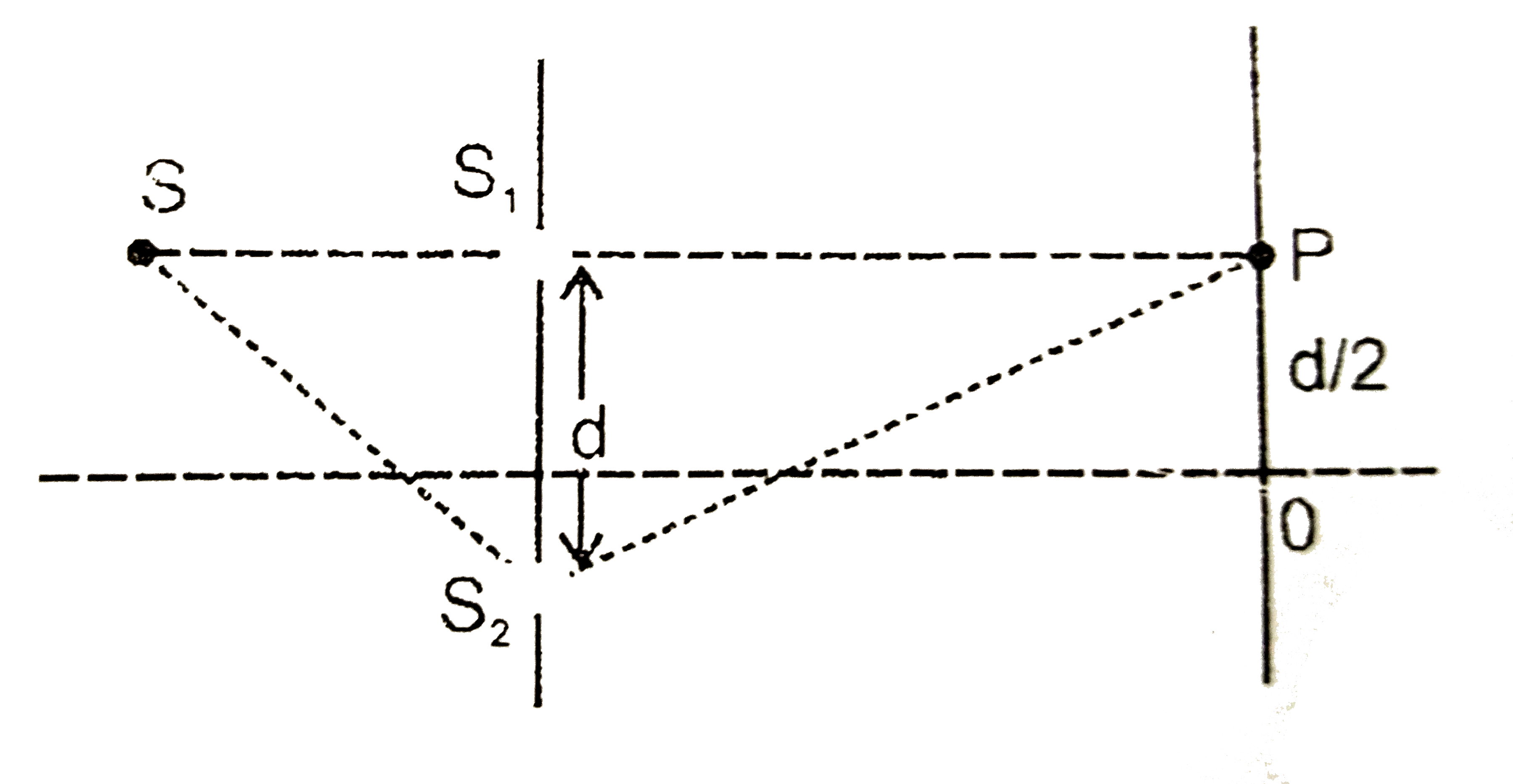
at `O`, path difference
`=dsintheta` where `theta` is the angle as shown: `("as" gt gt d)`
so `DeltaP=d sintheta cong d tantheta approx (d.d//2)/(l)=(d^(2))/(2l)`
`rArr Deltaphi =(2pi)/(lambda)xx(d^(2))/(2l)=(pid^(2))/(lambdal)`.
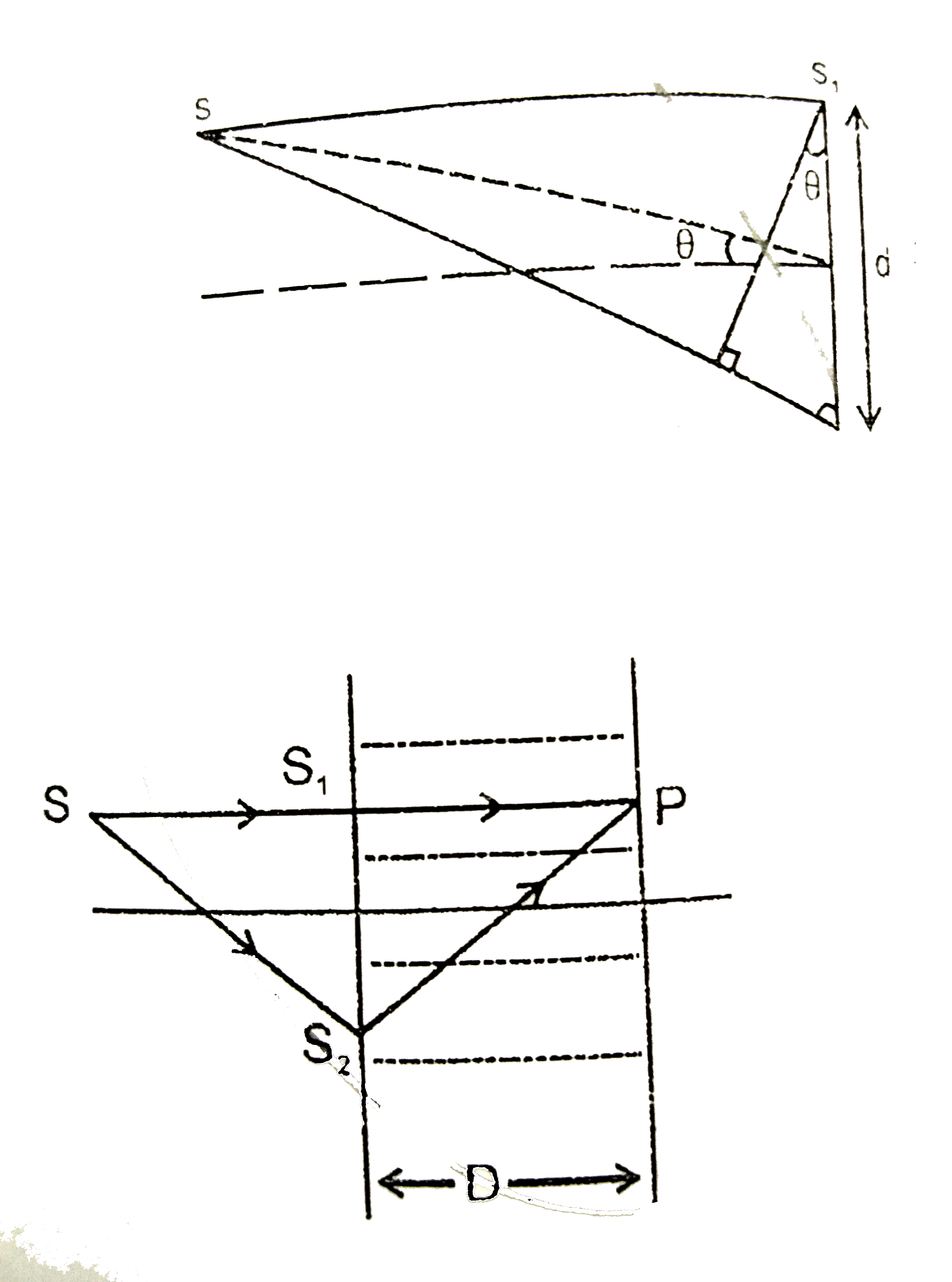
(a) Now if a liquid is flled as shown.
path defference `=(SS_(2)-SS_(1))+S_(2)P-S_(1)P`
`=(d^(2))/(dl)+(d^(2))/(2D)`
`rArr` phase difference `=(d^(2))/(2l)xx(2pi)/(lambda)+(d^(2))/(2D)xx(2pi)/((lambda//mu))`
`=(d^(2)pi)/(lambda)((1)/(l)+(mu)/(D))`
(b) `(i)` if liquid is filled on the left side.
`Deltaphi=(d^(2))/(2l)xx(2pi)/(lambda//mu)+(d^(2))/(2D)xx((2pi)/(lambda))=(pid^(2))/(lambda)((mu)/(l)+(1)/(D))`
(ii) Clearly it is asking about `beta//2 {therefore lambda lt lt d}`.
`rArr D_(min)=(beta)/(2)=(lambdaD)/(2d)`