Initially the 900μF capacitor is charged to 100 V and the 100μF capacitor is uncharged in the figure shown. Then the switch S2 is closed for a time t1, after which it is opened and at the same instant switch S1 is closed for a time t2 and then opened. It is now found that the 100μF capacitor is charged to 300 V. If t1andt2 minimum possible values of the time intervals, then findout t1t2

The correct Answer is:C
Step by step video, text & image solution for Initially the 900muF capacitor is charged to 100 V and the 100muF capacitor is uncharged in the figure shown. Then the switch S_(2) is closed for a time t_(1), after which it is opened and at the same instant switch S_(1) is closed for a time t_(2) and then opened. It is now found that the 100muF capacitor is charged to 300 V. If t_(1) and t_(2) minimum possible values of the time intervals, then findout (t_(1))/(t_(2)) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-2 PART 3
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-2 PART 4
Explore 6 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCEChapter:ELECTROMAGNETIC INDUCTIONExercise:Exercis-2 PART 1
Explore 15 Videos
- ELECTRODYNAMICSBook:RESONANCEChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTROSTATICSBook:RESONANCEChapter:ELECTROSTATICSExercise:HLP
Explore 39 Videos
Similar Questions
Initially the 900μF capacitor is charged to 100V and the 100μFcapacitor is uncharged in Fig. Then switch S2 is closed for time t1, after which it is opened and at the same instant switch S1 is closed for time t2 and then opened. It is now found that 100μF capacitor is charged to 300μF capacitor is charged to 300V. Find the minimum possible value of the time interval t1 and t2.

View SolutionA 20μF capacitor charged to 100 V is connected in parallel to a 10μF capacitor charged to 100 V. find the loss in energy.
View Solution
Knowledge Check
At t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
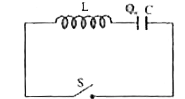 Aπ√LCB32π√LCCπ2√LCD2π√LC
Aπ√LCB32π√LCCπ2√LCD2π√LCIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
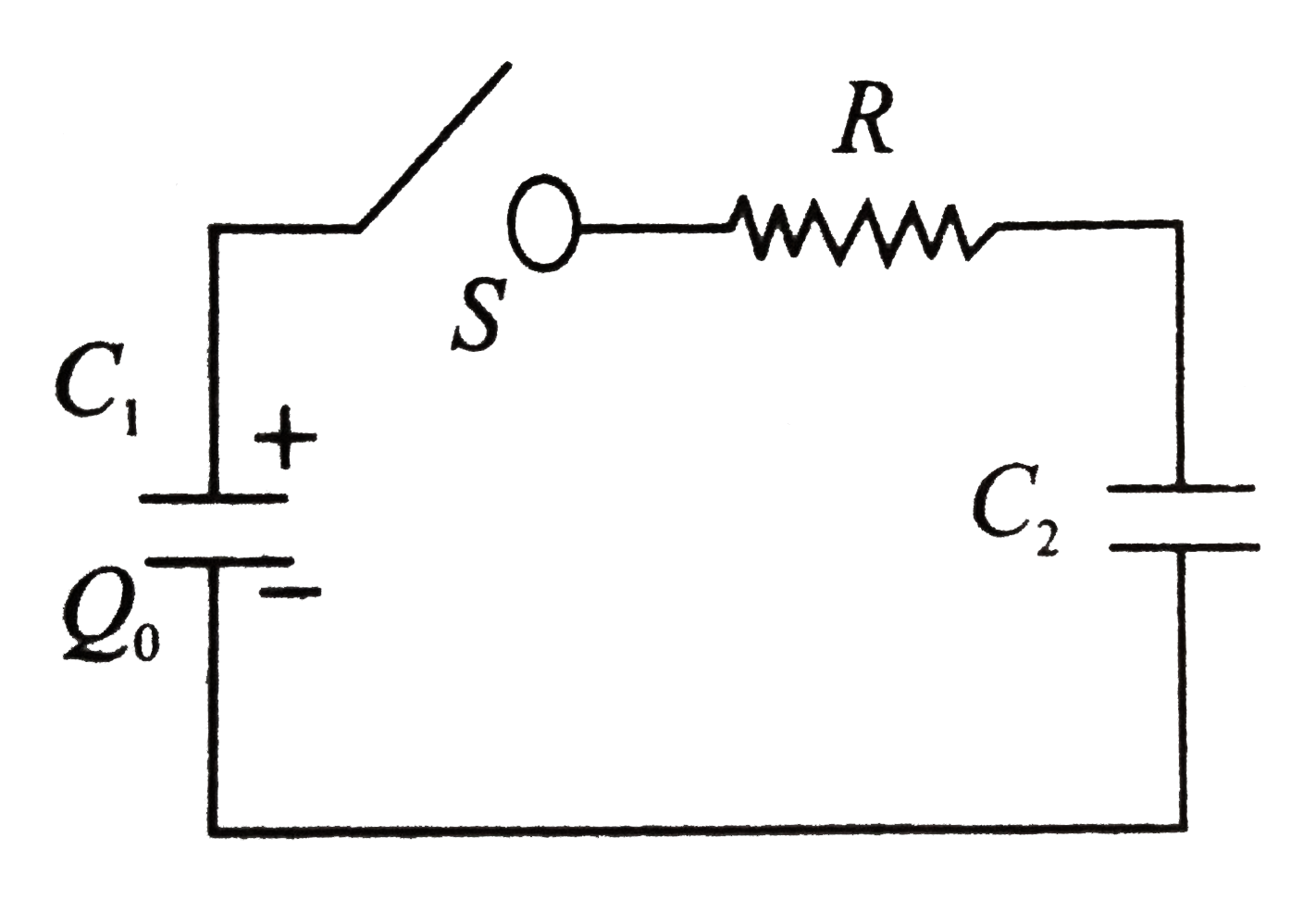 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)In the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
 ARCB3RCC23RCDRCIn(23)
ARCB3RCC23RCDRCIn(23)
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionIn the circuit shown. Initially the capacitor is uncharged. The switch S is closed at time t=0. Then
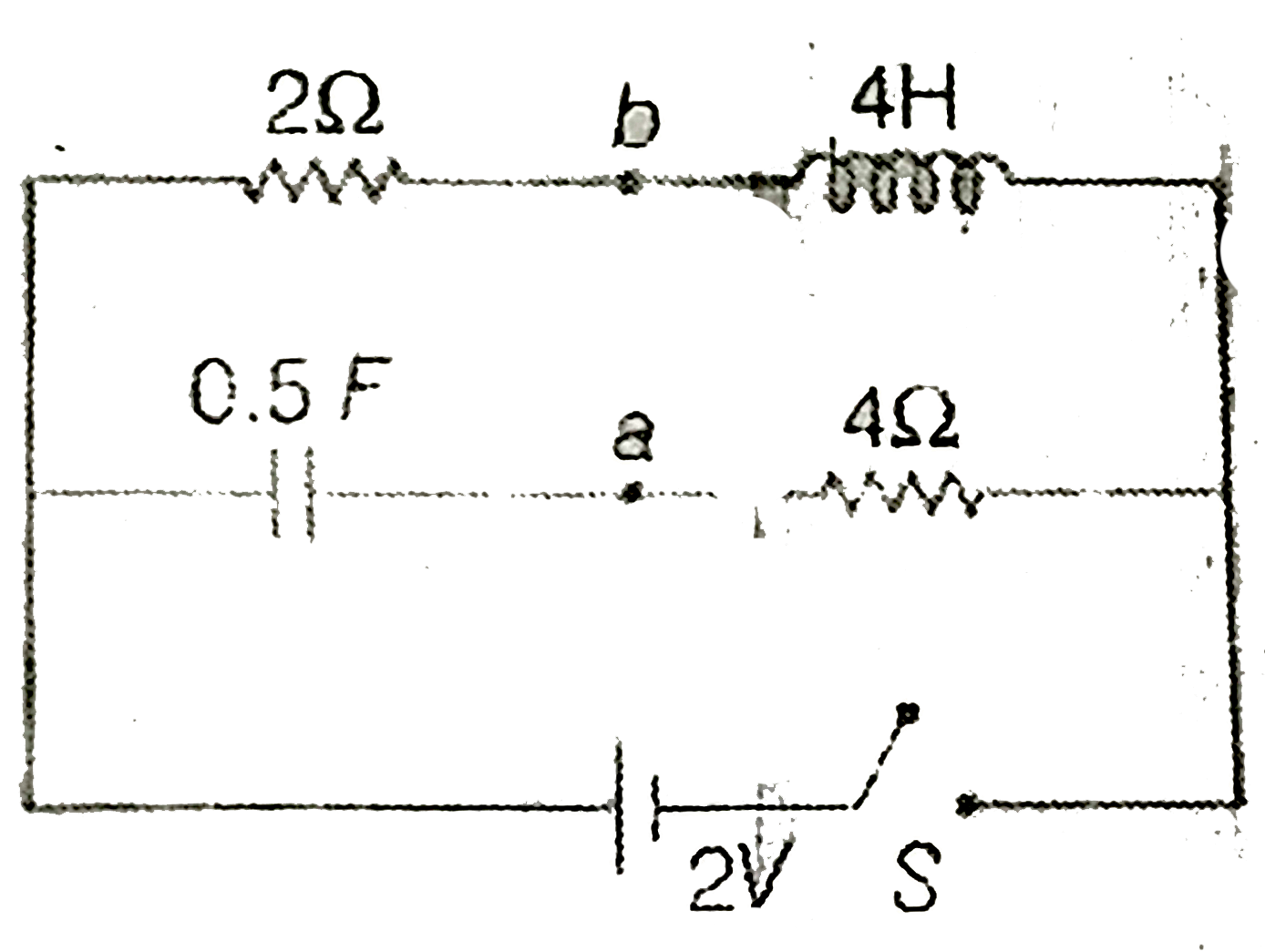
View SolutionIn the circuit shown, the capacitor is initially uncharged. The switch S is closed at t = 0. Time after which voltage across capacitor and resistor are equal is:
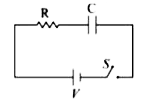
View Solution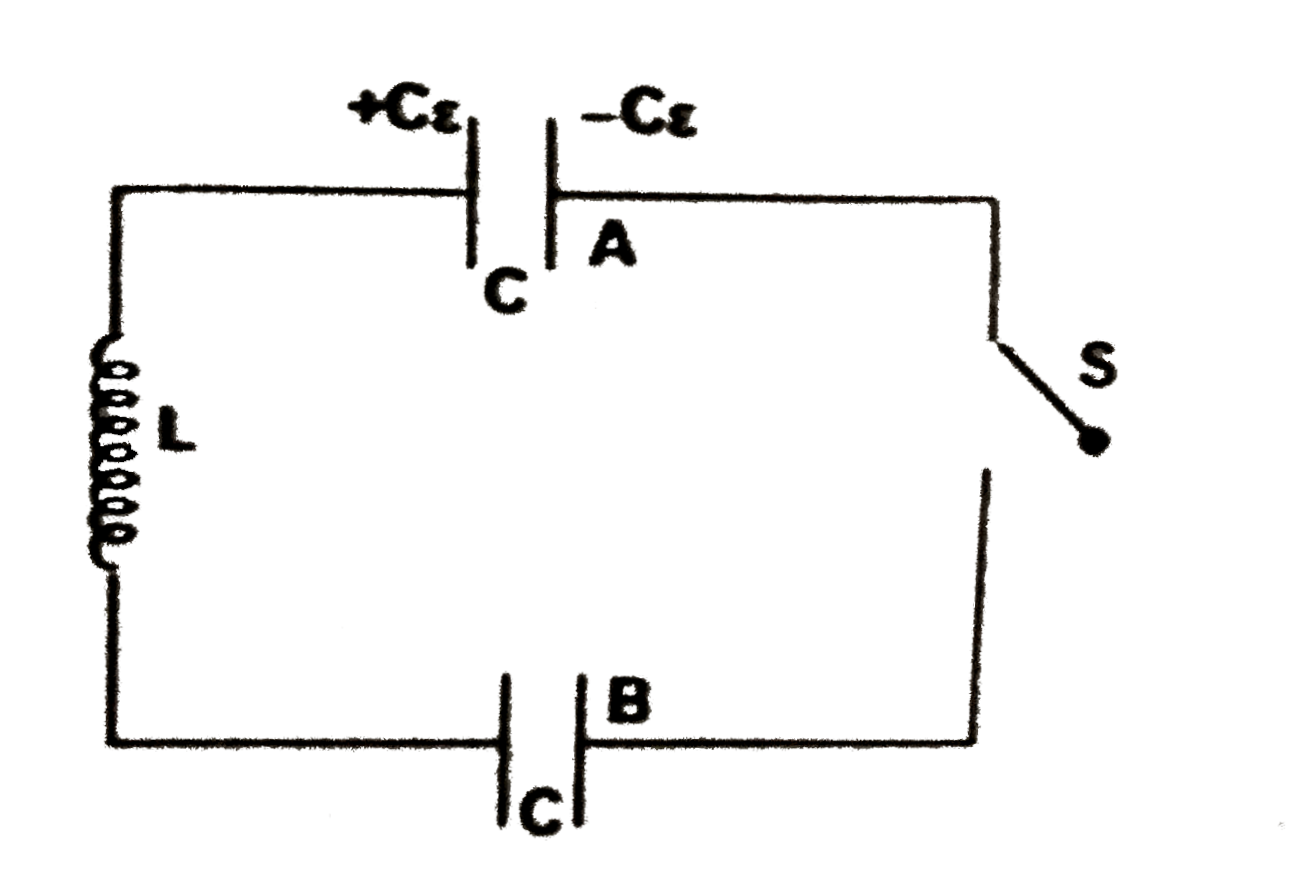
Initially capacitor 'A' is charged to a potential drop ε and capacitor B is uncharged At t=0, switch S is closed, then the maximum current through the inductor is
View SolutionA 2μF capacitor C1 is charge to a voltage 100 V and a 4μF∩aci→rC_2ischar≥d→avo<as≥50 V. The capacitors are then connected in parallel What is the loss of energy due to parallel connection?
View Solution
