Initially the 900μF capacitor is charged to 100V and the 100μFcapacitor is uncharged in Fig. Then switch S2 is closed for time t1, after which it is opened and at the same instant switch S1 is closed for time t2 and then opened. It is now found that 100μF capacitor is charged to 300μF capacitor is charged to 300V. Find the minimum possible value of the time interval t1 and t2.

Initial energy stored in the 900μF capcitor is
U1=(1/2)×900×10−6×(100)2=4.5J
Finally, energy stored in the 100μF capacitor is
U2=(1/2)×100×10−6×(300)2=4.5J
The entire energy of the 900μf capacitor has been transferred to the 100μF capacitor. First, electrical energy of the 900μF capacitor is converted into magnetic energy in the inductor and then this energy is converted into electrical energy once again using S2 and S1 appropriately.
In an LC circuit, the transfer of electrical energy into magnetic energy and vice verse takes place in time T/4 where T=2π√LC is time period of the electrical oscillations. Thus,
T12π√10×900×10−6=0.6s
T22π√10×100×10−6=0.2s
Therefore, switch S2 is first closed for time 0.6/4=0.15s, during which time the 900μF capacitor gets fully discharged and the current in the inductor is fully established. Next switch S2 is opened and simultaneously switch S1 is closed for time 0.2/4=0.05 s during which the current in the inductor disappears and the 100μF capacitor gets fully charged.
After this time, switch S1 is also opened. The 100μF capacitor is now charged to 300V.
Thus, t1=0.15s and t2=0.05s
Topper's Solved these Questions
- INDUCTANCEBook:CENGAGE PHYSICSChapter:INDUCTANCEExercise:Solved Examples
Explore 3 Videos
- INDUCTANCEBook:CENGAGE PHYSICSChapter:INDUCTANCEExercise:Exercise 4.1
Explore 24 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICSChapter:HEATING EFFECT OF CURRENTExercise:Thermal Power in Resistance Connected in Circuit
Explore 28 Videos
- KINETIC THEORYBook:CENGAGE PHYSICSChapter:KINETIC THEORYExercise:Question Bank
Explore 31 Videos
Similar Questions
Initially the 900μF capacitor is charged to 100 V and the 100μF capacitor is uncharged in the figure shown. Then the switch S2 is closed for a time t1, after which it is opened and at the same instant switch S1 is closed for a time t2 and then opened. It is now found that the 100μF capacitor is charged to 300 V. If t1andt2 minimum possible values of the time intervals, then findout t1t2

View SolutionIn the circuit shown , charge on the 5μF capacitor is :
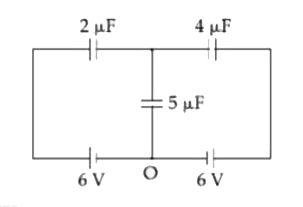
View Solution
Knowledge Check
In given circuit, ratio of charge on 2 μF capacitor to the charge of 3 μ F capacitor will be
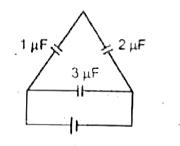 A2:3B3:2C1:9D2:9
A2:3B3:2C1:9D2:9In the given circuit, the charge on 4μF capacitor will be :
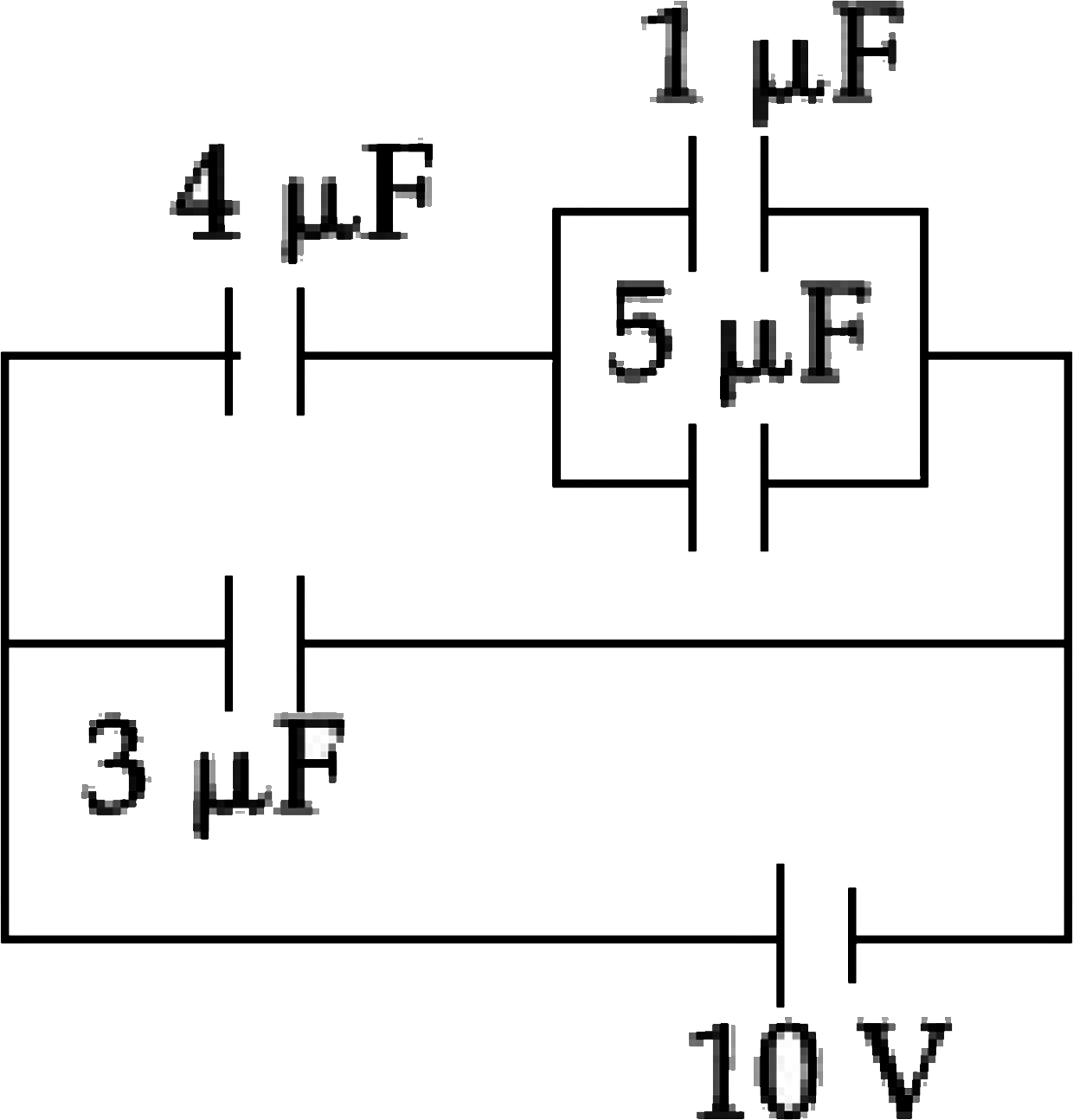 .A5.4μCB9.6μCC13.4μCD24μC
.A5.4μCB9.6μCC13.4μCD24μCIn the circuit in Fig. switch S1 was closed for a long time . At time t=0 the switch is opened.
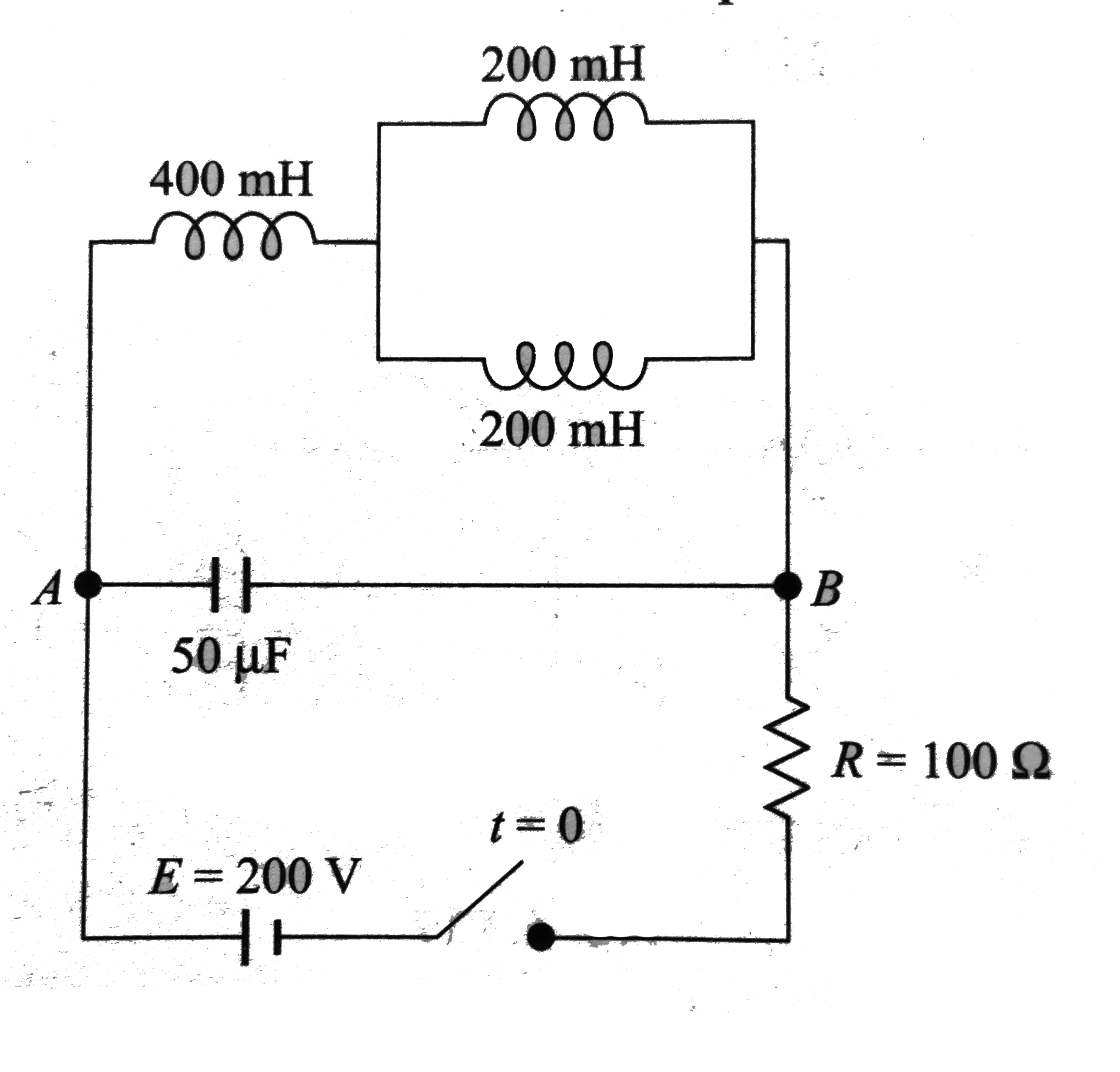
Find the angular frequency of oscillation of the charge on the capacitor.A100rads−1B200rads−1C300rads−1sD400rads−1
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionThe charge in the 2μF capacitor at steady state is
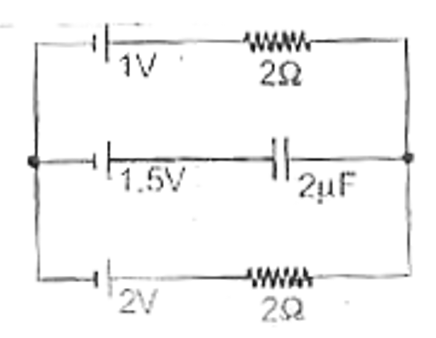
View SolutionIn the given circuit find out charge on 6μF and 1μF capacitor.

View SolutionAt t<0, the capacitor is charged and the switch is opened.At t=0 the switch is closed.The shortest time T at which the charge on the capacitor will be zero is given by:
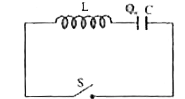
View SolutionIn the arrangement shown in in the switch S is , find

the final charge on the 6μF capacitor
View Solution

