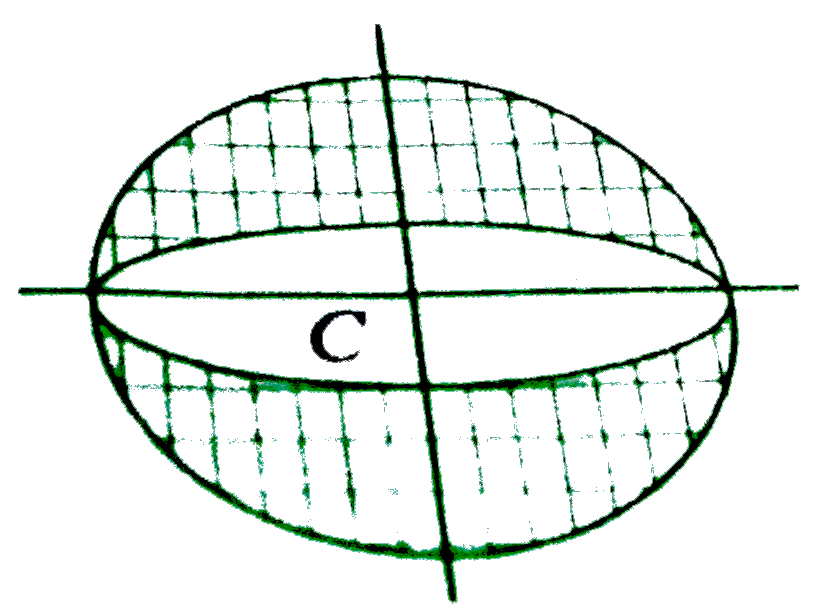
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
Two persons A and B agree to meet at a place between 5 and 6 pm. The first one to arrive waits for 20 min and then leave. If the time of their arrival be independant and at random, then the probability that A and B meet is
1/3
1/3
2/3
5/9
The correct Answer is:D

Let A and B arrive at the place of their meeting 'a' minute and 'b' minute after 5 pm. Their meeting is possible only if |a−b|≤20
Clearly, 0≤a≤60 and 0≤b≤60. Therefore, a and b can be selected as an ordered pair (a,b) from the set [0.60]×[0.60]. Alternatively, it is equivalent to select a point (a, b) from the square OPQR, where P is (60, 0) and R is (0, 60) in the Cartesian plane. Now,
|a−b|≤20⇒−20≤a−b≤20
Therefore, points (a, b) satisfy the equation −20≤x−y≤20. Hence, favorable condition is equivalent to selecting a point from the region bounded by y≤x+20 and y≥x−20. Therefore, the required probability is
Area of OABQCDOArea of square OPQR=[Ar(OPQR)−2Ar(ΔAPB)]Ar(OPQR)
=60×60−22×40×4060×60=59
Topper's Solved these Questions
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise (Matrix)
Explore 2 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise (Numerical)
Explore 7 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise (Multiple)
Explore 8 Videos
- PROBABILITY AND STATISTICSBook:CENGAGEChapter:PROBABILITY AND STATISTICSExercise:Question Bank
Explore 37 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:NUMARICAL VALUE TYPE
Explore 2 Videos
Similar Questions
An ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. Let the probability that this point lies outside the ellipse be p. Then the value of 105 p is
View SolutionAn ellipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. Let the probability that this point lies outside the ellipse be p. Then the value of 105 p is
View Solution
Knowledge Check
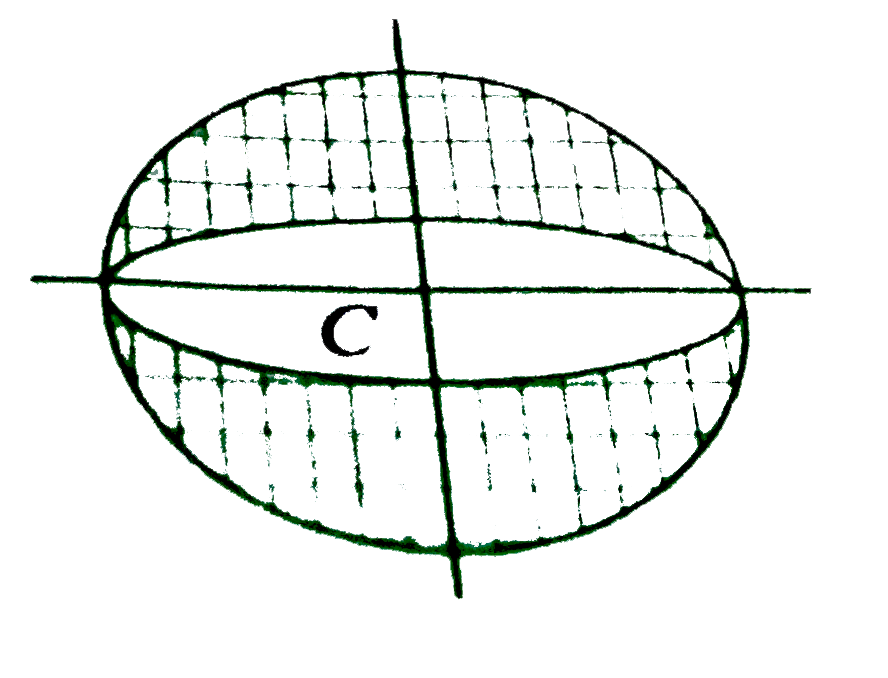
There are some experiment in which the outcomes cannot be identified discretely. For example, an ellipse of eccentricity 2√2/3 is inscribed in a circle and a point within the circle is chosen at random. Now, we want to find the probability that this point lies outside the ellipse. Then, the point must lie in the shaded region shown in Figure. Let the radius of the circle be a and length of minor axis of the ellipse be 2b. Given that
1−b2a2=89orb2a2=19
Then, the area of circle serves as sample space and area of the shaded region represents the area for favorable cases. Then, required probability is
p=Area of shaded regionArea of circle
=πa2−πabπa2=1−ba=1−13=23
Now, answer the following questions.
A point is selected at random inside a circle. The probability that the point is closer to the center of the circle than to its circumference isA1/4B1/2C1/3D1/√2An eppipse of eccentricity 2√23 is inscribed in a circle and a point within the circle is chosen at random. The probability that this point lies outside the ellipse is
A1/9B4/9C1/3D2/3An ellipse of eccentricity 2√23 is inscribed in a circle . A point is chosen inside the cirlce at random. The probaboility that the point lies outside the ellipse is
A12B23C19D29
An ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is 23 then the eccentricity of the ellipse is: (A) 2√23 (B) √53 (C) 89 (D) 23
View SolutionAn ellipse is inscribed in a circle and a point within the circle is chosen at random. If the probability that this point lies outside the ellipse is 23 then the eccentricity of the ellipse is: (A) 2√23 (B) √53 (C) 89 (D) 23
View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 1
View SolutionAn ellipse is inscribed in its auxiliary circle and a point within the circle is chosen at random. If p is the probability that this point lies outside the ellipse and inside the auxiliary circle. Then 8p is equal to (where eccentricity of the ellipse is √32)
(A) 3 (B) 4 (C) 6 (D) 1
View SolutionA point is chosen at random inside a circle. Find the probability that the point is closer to the centre of the circle than to its circumference.
View Solution

