There are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then
When x = 4, then P(E) is equal to
5/9
6/7
7/18
8/19
The correct Answer is:C
The number of ways in which different sums can occurs is (3 + 2 + 1)(1 + 2 + 3) = 36. The probability of 4 is 14/36=7/18.
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Matrix)
2 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Numerical)
7 Videos
- PROBABILITY I BOOK - CENGAGECHAPTER - PROBABILITY I EXERCISE - Exercise (Multiple)
8 Videos
- PROBABILITY AND STATISTICSBOOK - CENGAGECHAPTER - PROBABILITY AND STATISTICSEXERCISE - Question Bank
37 Videos
- PROBABILITY IIBOOK - CENGAGECHAPTER - PROBABILITY IIEXERCISE - NUMARICAL VALUE TYPE
2 Videos
Similar Questions
A dice marked with digit {1,2,2,3,3,3}, thrown three times, then the probability of getting sum of number on face is six, is equal to ;- 7216
View SolutionA ordinary cube has four plane faces, one face marked 2 and another face marked 3, find the probability of getting a total of 7 in 5 throws.
View Solution
Knowledge Check
There are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then P(E) is maximum when x equal to
A5B3C4D6There are two die A and B both having six faces. Die A has three faces marked with 1, two faces marked with 2, and one face marked with 3. Die B has one face marked with 1, two faces marked with 2, and three faces marked with 3. Both dices are thrown randomly once. If E be the event of getting sum of the numbers appearing on top faces equal to x and let P(E) be the probability of event E, then P(E) is minimum when x equals to
A3B4C5D6The mean of the numbers obtained on throwing a die having written 1 one three faces, 2 on two faces and 5 on one face is
A2B3C4D5
The net shown below can be folded into the shape of a cube. The face marked with the letter L is opposite to the face marked with which letter?
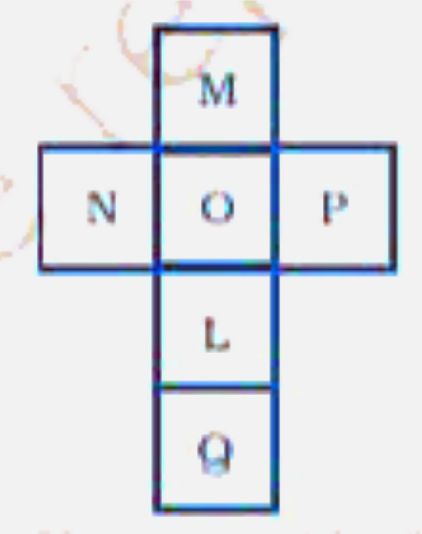
View SolutionD1,D2 are two cubical dice, with faces of D1 marked 1,2,2,3,3,3 and faces of D2 marked 1,1,2,2,3,3. One of the 2 dice is selected at random and tosses 3 times. If the sum of the numbers obtained is equal to 6 then the probability that the selected die is D1 is
View SolutionA six-faced unbiased die is thrown twice and the sum of the numbers appearing on the upper face is observed to be 7. The probability that the number 3 has appeared atleast once, is
View SolutionA six -faced unbiased die is thrown twice and the sum of the numbers appearing on the upper face is observed to be7. The probability that the number 3 has appeared at least one ,is
View SolutionA dice has four blank faces and two faces marked 3. The change of getting a total of 12 in 5 throws is
View Solution
