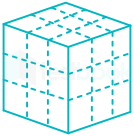
A cube having all of its sides painted is cut by two horizontal, two vertical, and other two planes so as to form 27 cubes all having the same dimensions. Of these cubes, a cube is selected at random.
The probability that the cube selected has none of its sides painted is
A
1/9
B
1/27
C
1/18
D
5/54
Video Solution
Text Solution
The correct Answer is:B
Clearlly, cube at the centre is the only cube which is not painted. On each edge, we have one cube pained on two sides. So, there are twelve cubes pained on two sides.
|
Topper's Solved these Questions
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise (Matrix)
Explore 2 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise (Numerical)
Explore 7 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise (Multiple)
Explore 8 Videos
- PROBABILITY AND STATISTICSBook:CENGAGEChapter:PROBABILITY AND STATISTICSExercise:Question Bank
Explore 37 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:NUMARICAL VALUE TYPE
Explore 2 Videos
Similar Questions
Knowledge Check
A cube having all of its sides painted is cut by two horizontal, two vertical, and other two planes so as to form 27 cubes all having the same dimensions. Of these cubes, a cube is selected at random.
The probability that the cube selected has two sides painted isA1/9B4/9C8/27Dnone of theseA cube having all of its sides painted is cut to be two horizontal , two vertical and other two planes, so as to form 27 cubes all having the same dimesions of these cubes, a cube is selected at random.
If P3 be the probability that the cube selected has none of its sides painted, then the value of 27P3, isA1B2C3D5A cube having all of its sides painted is cut by two horizontal, two vertical, and other two planes so as to form 27 cubes all having the same dimensions. Of these cubes, a cube is selected at random.
The total number of cubes having at least one of its sides painted isA18B20C22D26
The side of a cube having volume 27 cm3 is
View SolutionA cube of edge 6 cm is painted on all sides and then cut into units cubes. The number of unit cubes with no sides painted is
View SolutionTwo cubes have their volume in the ratio 1:27. The ratio of their surface areas is
View SolutionTwo cubes have their volume in the ratio 1:27. The ratio of their surface areas is
View SolutionA cube of 3" × 3" × 3" inch size was painted on all six sides and then cut into 27 small cubes of 1 inch size. How many smaller cubes will have only two sides painted?
View Solution

