Let P(x) denote the probability of the occurrence of event x. Plot all those point (x y) = (P(A), P(B)) in a plane which satisfy the conditions, P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8
P(A∪B)≥34and18≤P(A∩B)≤38
Hence,
P(A)+P(B)−P(A∩B)≤34
implies P(A)+P(B)≥34+P(A∩B)≥34+18=78
⇒x+y≥78
We know that
P(A∩B)≤1
⇒P(A)+P(B)≤1+P(A∩B)≤1+38=118
⇒x+y≤118
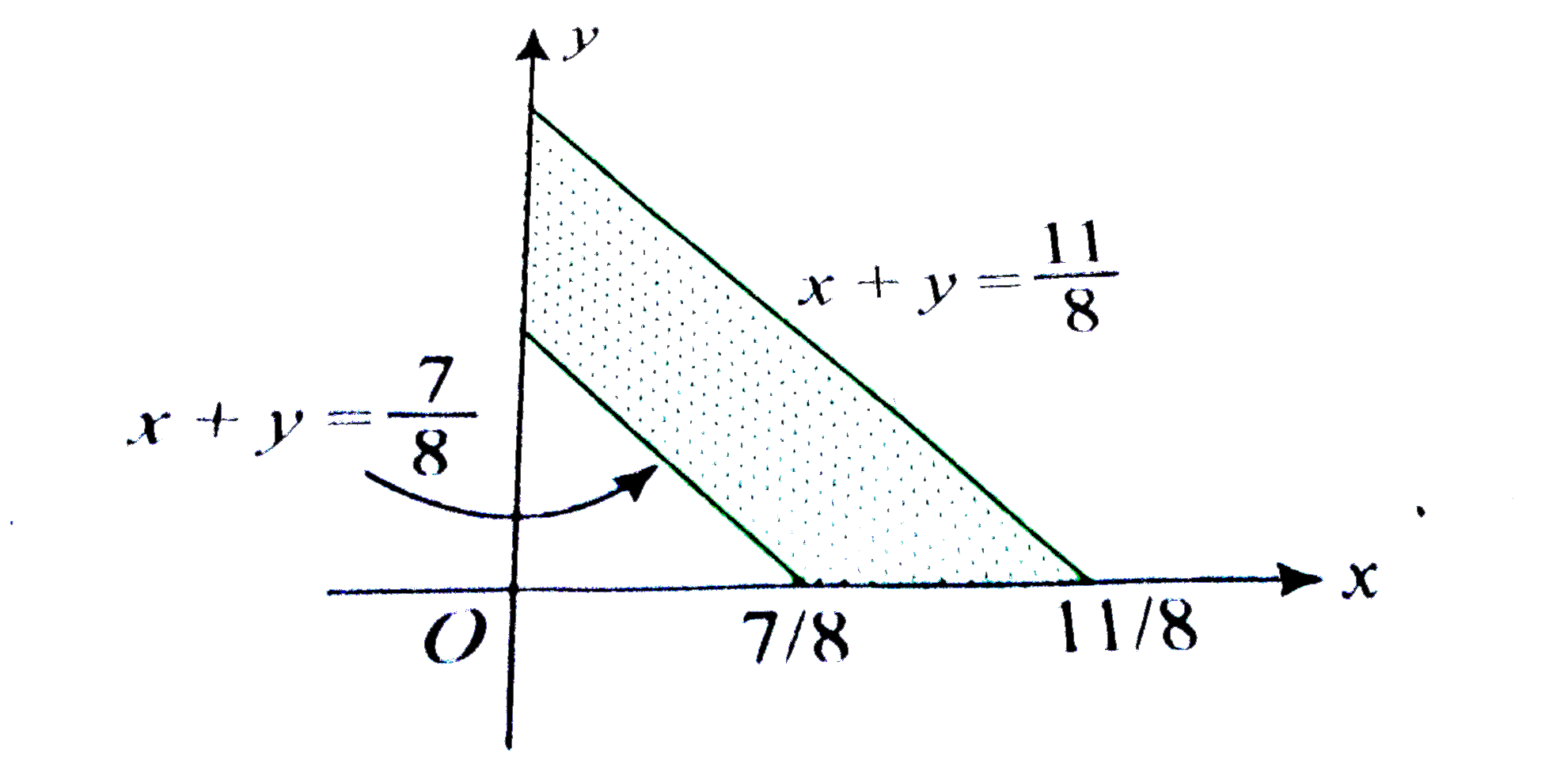
The shaded part in the figure is the required region.
Topper's Solved these Questions
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise 9.1
Explore 6 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise 9.2
Explore 19 Videos
- PROBABILITY AND STATISTICSBook:CENGAGEChapter:PROBABILITY AND STATISTICSExercise:Question Bank
Explore 37 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:NUMARICAL VALUE TYPE
Explore 2 Videos
Similar Questions
Knowledge Check
If A and B are two events such that P(A∪B)=3/4,P(A∩B)=1/4,P(A')=2/3 , then P(A'∪B) is
A512B38C58D14The following question consist of two statements, one labelled as the 'Assertion (A)' and the other as 'Reason (R)' You are to examine these two statements carefully and select the answer.
Assertion (A) : If P(A)=34andP(B)=38, then
P(A∪B)≥34
Reason (R) : P(A)≤P(A∪B)andP(B)≤P(A∪B), hence
P(A∪B)≥ max .{P(A),P(B)}ABoth A and R are individually true, and R is the correct explanation of A.BBoth A and R are individually true but R is not the correct explanation of A.CA is true but R is false.DA is false but R is true.
Let P(E) denote the probability of occurrence of event E. If A and B are two events associated with an experiment such that ∣∣ ∣ ∣∣P(A)−1P(B)−P(A∩B)P(B)−P(A∩B)P(A)−1−P(A∩B)P(A)−1P(B)∣∣ ∣ ∣∣=0 then
(A) P(A∪B)=1
(B) P(AB)=P(A)+P(B)−1P(B)
(C) if A⊂B then P(B)=P(A∪B)
(D) if A⊂B then P(A)=1
View SolutionLet P(E) denote the probability of occurrence of event E. If A and B are two events associated with an experiment such that, ∣∣ ∣ ∣∣P(A)−1P(B)−P(A∩B)P(B)−P(A∩B)P(A)−1−P(A∩B)P(A)−1P(B)∣∣ ∣ ∣∣=0 ,then
(A) P(A∪B)=1
(B) P(AB)=P(A)+P(B)−1P(B)
View SolutionIf A,B are two eevts such that P(A∪B)≥34and18≤P(A∩B)≤38 then
View SolutionLet A and B be two independent events. The probability of their simultaneous occurrence is 1/8 and the probability that neither occurs is 3/8. Find P(A)andP(B).
View SolutionIf P is a probability function, show that for any two events A, B. P(A∩B)≤P(A)≤P(A∪B)≤P(A)+P(B)
View SolutionA,B are two events such that P(A∪B)≥34 and 18≤P(A∩B)≤38 then P(A)+P(B)∈
View Solution