Which of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
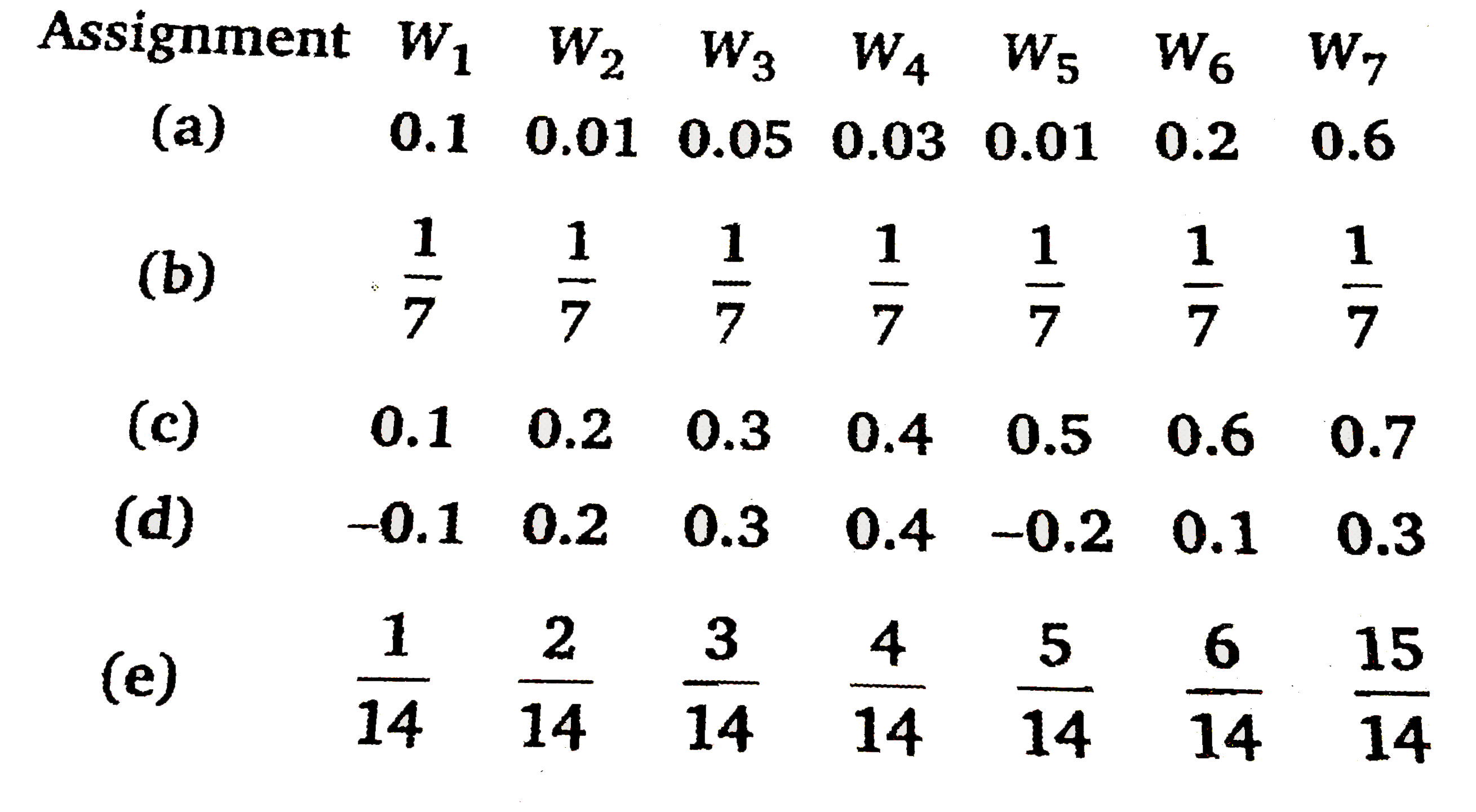
The correct Answer is:(c ), (d) and (e)
(a) In assignment (a), each number is positive and less and 1 Sum of probailities
= 0.1 + 0.01 + 0.05 + 0.03 + 0.01 + 0.2 + 0.6 = 1
Thus, this assignment is valid.
(b) In assignment (b), each number is positive and less than 1.
Sum of probabilities = 17+17+17+17+17+17+17=7×17=1
Thus, this assignment is valid.
(c ) In assignment (c ), each number is positive and less and 1 Sum of probabilities.
= 0.1 + 0.2 + 0.3 + 0.4 + 0.5 + 0.6 + 0.7 = 28 ≠ 1
Thus, the assignment is not valid.
(d) In assignment, two numbers are negative. So, it is not valid assignment.
(e) In assignment, p(ω7)=1514>1. So, it is not valid assignment.
Topper's Solved these Questions
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise 9.2
Explore 19 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:Exercise 9.3
Explore 7 Videos
- PROBABILITY I Book:CENGAGEChapter:PROBABILITY I Exercise:JEE Advanced Previous Year
Explore 7 Videos
- PROBABILITY AND STATISTICSBook:CENGAGEChapter:PROBABILITY AND STATISTICSExercise:Question Bank
Explore 37 Videos
- PROBABILITY IIBook:CENGAGEChapter:PROBABILITY IIExercise:NUMARICAL VALUE TYPE
Explore 2 Videos
Similar Questions
Which of the following can be the valid assignment of probability for outcomes of sample space, S={W1,W2,W3},{ where W1,W2 and W3 are mutually exclusive events
Assignment
w1w2w3(a)0.40.20.8(b)001(c)−123412(d)121214
View SolutionWhich of the following cannot be valid assignment of probability for elementary events or outcomes of samples space S={w1,w2,w3,w4,w5,w6,w7}: Elementary events w1 w2 w3 w4 w5 w6 w7 i. 0.1 0.01 0.05 0.03 0.01 0.2 0.6 ii. 17 17 17 17 17 17 17 iii. 0.7 0.6 0.5 0.4 0.3 0.2 0.1 iv. 114 214 314 414 514 614 1514
View Solution
Knowledge Check
The weight of an object in the coal mine, sea level and at the top of the mountain are W1,W2 and W3 respectively, then
AW2>W1>W3BW1=W2=W3CW1<W2<W3DW1>W2>W3If W1:W2=2:3 and W1:W3=1:2, then W2:W3 is:
A3:4B4:3C2:3D4:5If W1:W2=2:3 and W1:W3=1:2 then W2:W3 is
A3:4B4:3C2:3D4:5
[W_(1),W_(2),W_(3)" are apparent "],[" weights of a solid in water at "],[0^(0)C,4^(0)c" and "50^(0)c],[" respectively.If expansion of "],[" solid is negligible,then "],[" A) "W_(1)=W_(2)=W_(3)],[" B) "W_(1)>W_(2)>W_(3)],[" C) "W_(3)>W_(1)>W_(2)],[" D) "W_(3)>W_(2)>W_(1)]
View SolutionLet w be the 7th root of unity then log3∣∣∣1+w+w2+w3+w4+w5−8w∣∣∣=
View SolutionIf ω is a cube root of unity, then find the value of the following: (1+ω−ω2)(1−ω+ω2)
View SolutionIf w is a complex cube root of unity, then the value of the determinant
Δ=⎡⎢⎣1ww2ww21w21w⎤⎥⎦, is
View SolutionIf W1W2 and W3 represent the work done in moving a particle from A to B along three different paths 1.2 and3 respectively (as shown ) in the gravitational fieled of a point mass m, find the correct relation between W_(1) W_(2)andW_(3)
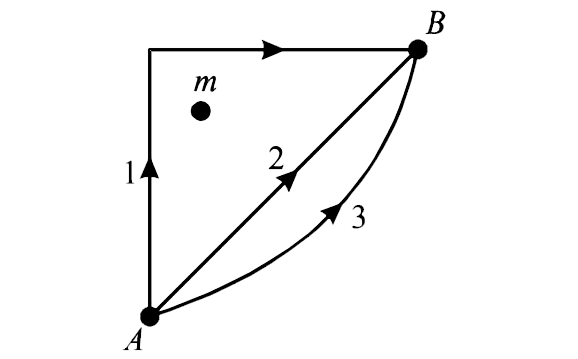
View Solution

