A simple pendulum executing $S H M$ in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line $O A B$ are 'a' and 'b'. If the velocity half wat between them is 'v' then its time period is

A

$\frac{π (b + a)}{v}$

B

$π (\frac{b - a}{v})$

C

$(\frac{b + a}{2 v})$

D

$(\frac{b - a}{2 v})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

A and B are the extreme position $\Rightarrow 2 A = b - a$
$\Rightarrow A = \frac{b - a}{2}$ is the amplitude
Halfway between them is the mean position $v = A ω$
$T = \frac{2 π}{ω} = \frac{2 π A}{v} = \frac{2 π}{v} (\frac{b - a}{2}) - \frac{π (b - a)}{v}$

|

Updated on:21/07/2023

Class 11 PHYSICS SIMPLE HARMONIC MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is executing SHM along a straight line. Its velocities at distances $x_{1}$ and $x_{2}$ from the mean position are $v_{1}$ and $v_{2}$ , respectively. Its time period is
A $2 π \sqrt{\frac{x_{1}^{2} + x_{2}^{2}}{v_{1}^{2} + v_{2}^{2}}}$
B $2 π \sqrt{\frac{x_{2}^{2} - x_{1}^{2}}{v_{1}^{2} - v_{2}^{2}}}$
C $2 π \sqrt{\frac{v_{1}^{2} + v_{2}^{2}}{x_{1}^{2} + x_{2}^{2}}}$
D $2 π \sqrt{\frac{v_{1}^{2} - v_{2}^{2}}{x_{1}^{2} - x_{2}^{2}}}$
Question 2 - Select One
Two particles are moving along a straight line as shown. The velocity of approach between A and B is

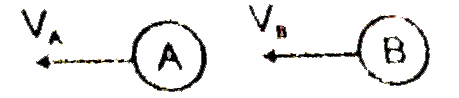A $V_{A} + V_{B}$
B $| V_{A} - V_{B} |$
C $V_{A} - V_{B}$
D $V_{B} - V_{A}$
Question 3 - Select One
A particle is moving on a straight line and its average velocity is found to be zero in an interval of time.
AAverage speed of the particle may also be zero for a given interval of time.
BVelocity of the particle can never be zero in given interval of time.
CVelocity of the particle must be zero at a particular instant.
DAcceleration of particle may be zero.

NARAYNA-OSCILLATIONS-EXERCISE - I (H.W)

Home
Ask Doubt
Profile