A load of mass M is attached to the bottom of a spring of mass 'M/3' and spring constant 'K'. If the system is set into oscillation, the time period of oscillation is
2π3√10M3K
4π√M3K
4π√MK
2π√M3K
The correct Answer is:A
Effective mass of a spring 13 actual mass
=13(M3)=M9
Total mass =M+M9=10M9
T=2π√10M9k=2π3√10Mk
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (C.W)
27 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - II (H.W)
19 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - I (C.W)
63 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Springs of spring constant k, 2k, 4k , 8k, …. Are connected in series. A block of mass 50 kg is attached to the lower end of the last spring and the system is set into oscillation. If k = 3.0 N/cm, what is the time period of oscillations ?
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution
Knowledge Check
A block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be
 A2π√m3kB2π√3m2kC2π√2m3kD2π√3km
A2π√m3kB2π√3m2kC2π√2m3kD2π√3kmA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is
 A2π√mkB2π√m2kC2π√m3kDπ√mk
A2π√mkB2π√m2kC2π√m3kDπ√mkA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
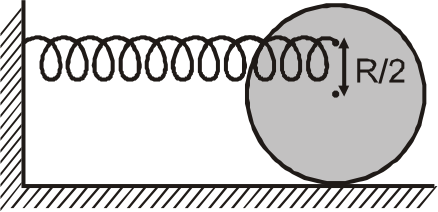 A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
A2π√mkB2π√2m3kCπ√3m2kDπ√2m3k
Springs of apring constants k,2k,4k,8k . . . Are connected in series. A mass m kg is attached to the lower end of the last spring and the system is allowed to vibrate. What is the time period of oscillations?
View SolutionSprings of spring constants k, 2k, 4k, 8k, …… are connected in series. A mass m kg is attached to the lower end of the last spring and the systemm is allowed to vibrate. What is the time period of oscillations? Given m=40gm,k=2.0Ncm−1.
View Solution
The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
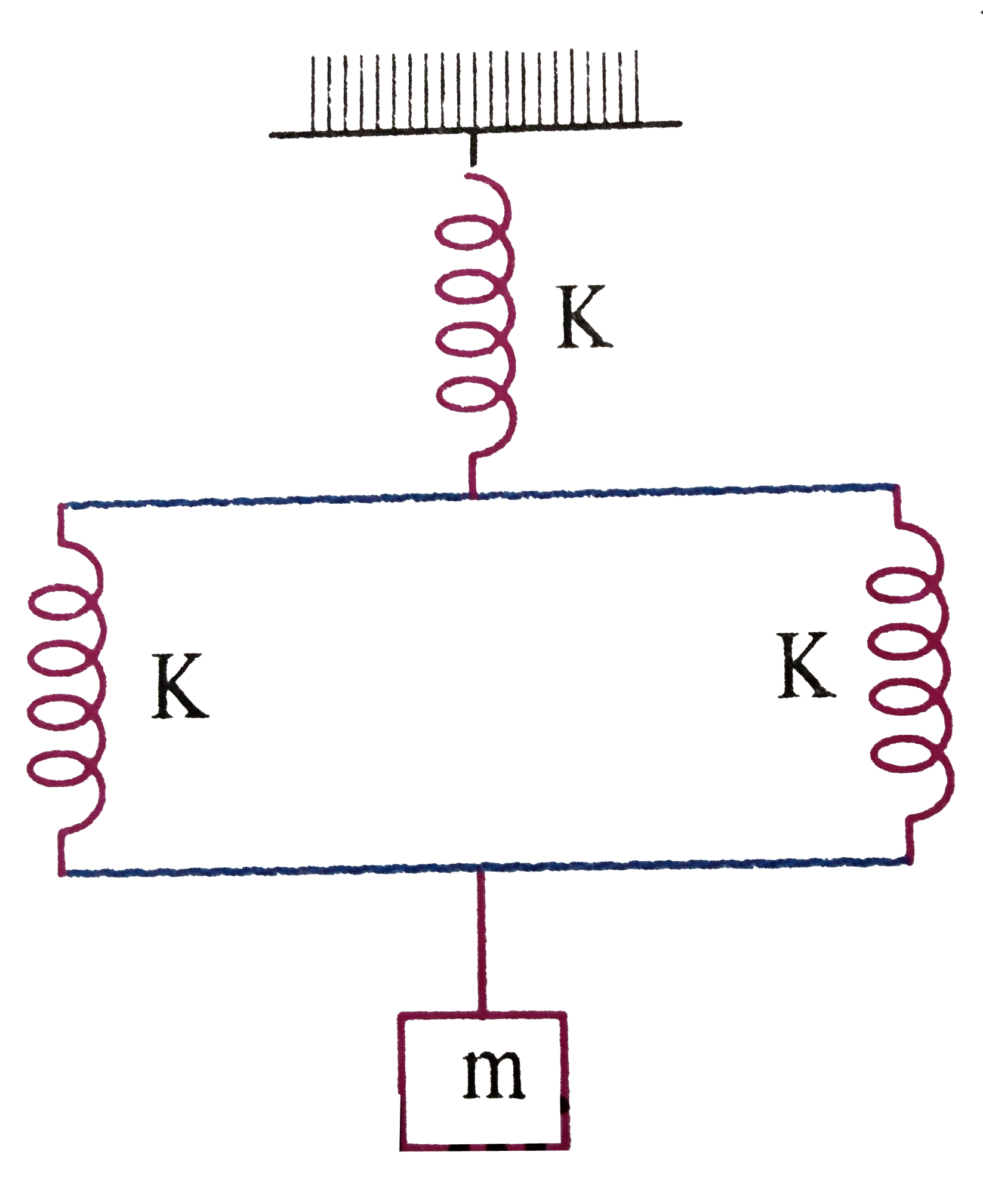
View Solution
