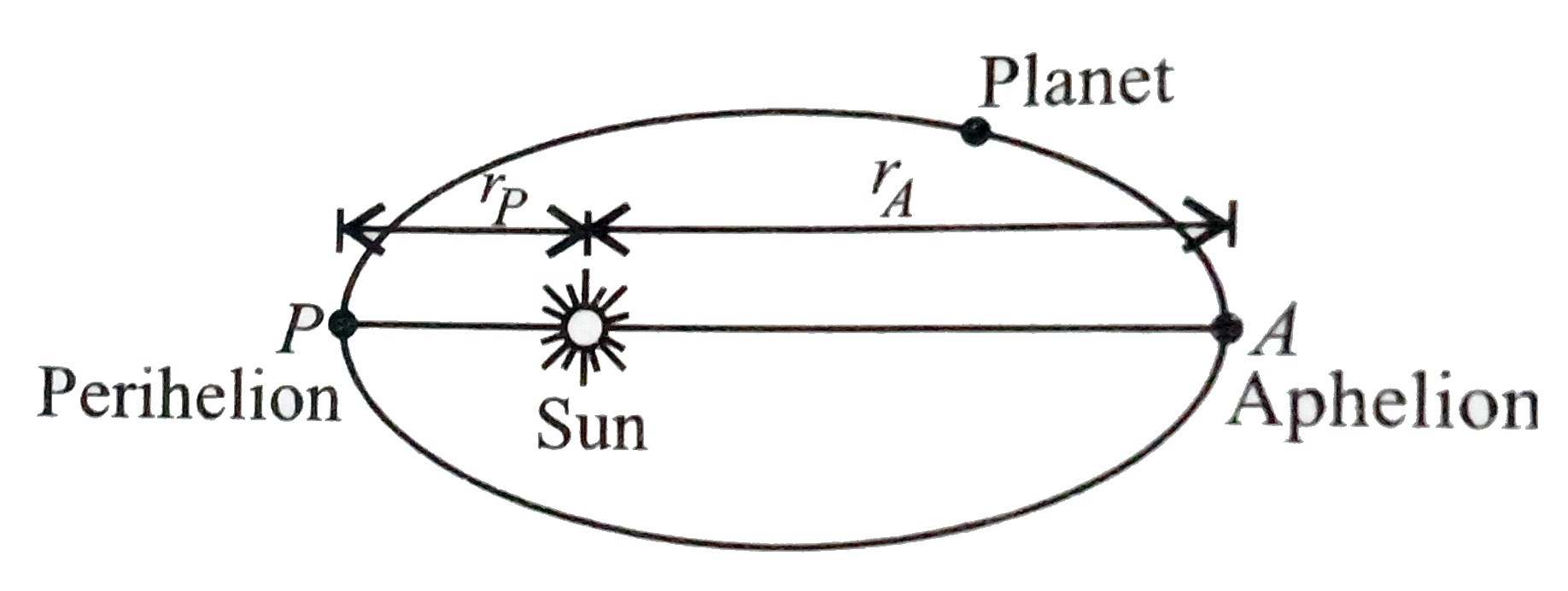
A speed of the palnet at the perihelion P be Vp and the sun -planet distance SP be rP as shown in fig. Relate {rp,vp} to the corresponding quantities at the aphelion {rA,VA}. Will the planet take equal times to traverse BAC and CPB?
To solve the problem, we need to relate the quantities at perihelion (point P) and aphelion (point A) for a planet orbiting the sun. We will also determine whether the time taken to traverse the arcs BAC and CPB is equal.
Step 1: Understand the conservation of angular momentum
The angular momentum L of a planet in orbit is given by the formula:
L=m⋅v⋅r
Where:
- m is the mass of the planet,
- v is the orbital speed,
- r is the distance from the sun.
Since there are no external torques acting on the planet, the angular momentum is conserved. Therefore, we can write:
m⋅VP⋅rP=m⋅VA⋅rA
Here, VP and VA are the speeds of the planet at perihelion and aphelion, respectively, and rP and rA are the corresponding distances from the sun.
Step 2: Simplify the equation
Since the mass m of the planet is constant, we can cancel it from both sides of the equation:
VP⋅rP=VA⋅rA
From this, we can express the relationship between the speeds and distances:
VPVA=rArP
Step 3: Determine the time taken to traverse arcs BAC and CPB
According to Kepler's second law (the law of areas), a line segment joining a planet to the sun sweeps out equal areas during equal intervals of time. This means that the time taken to traverse equal areas is the same.
1. Area BAC: The area swept out from point B to A and then to C.
2. Area CPB: The area swept out from point C to P and then to B.
Since both areas are equal (as they are sections of the same elliptical orbit), the time taken to traverse these arcs will also be equal.
Conclusion
Thus, we have established the relationships:
VPVA=rArP
And we conclude that the time taken to traverse arcs BAC and CPB is equal.
The angular momentum L of a planet in orbit is given by the formula:
L=m⋅v⋅r
Where:
- m is the mass of the planet,
- v is the orbital speed,
- r is the distance from the sun.
m⋅VP⋅rP=m⋅VA⋅rA
Here, VP and VA are the speeds of the planet at perihelion and aphelion, respectively, and rP and rA are the corresponding distances from the sun.
Since the mass m of the planet is constant, we can cancel it from both sides of the equation:
VP⋅rP=VA⋅rA
From this, we can express the relationship between the speeds and distances:
VPVA=rArP
According to Kepler's second law (the law of areas), a line segment joining a planet to the sun sweeps out equal areas during equal intervals of time. This means that the time taken to traverse equal areas is the same.
2. Area CPB: The area swept out from point C to P and then to B.
Thus, we have established the relationships:
VPVA=rArP
And we conclude that the time taken to traverse arcs BAC and CPB is equal.
Topper's Solved these Questions
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EVALUATE YOURSELF -1
3 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - EVALUATE YOURSELF -2
5 Videos
- GRAVITATIONBOOK - NARAYNACHAPTER - GRAVITATIONEXERCISE - LEVEL-VI
42 Videos
- FRICTIONBOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I
6 Videos
- KINETIC THEORY OF GASESBOOK - NARAYNACHAPTER - KINETIC THEORY OF GASESEXERCISE - LEVEL-III(C.W)
52 Videos
Similar Questions
Let the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View SolutionLet the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View Solution
Knowledge Check
P−T diagram is shown in Fig. Choose the corresponding V−T diagram.
 A
A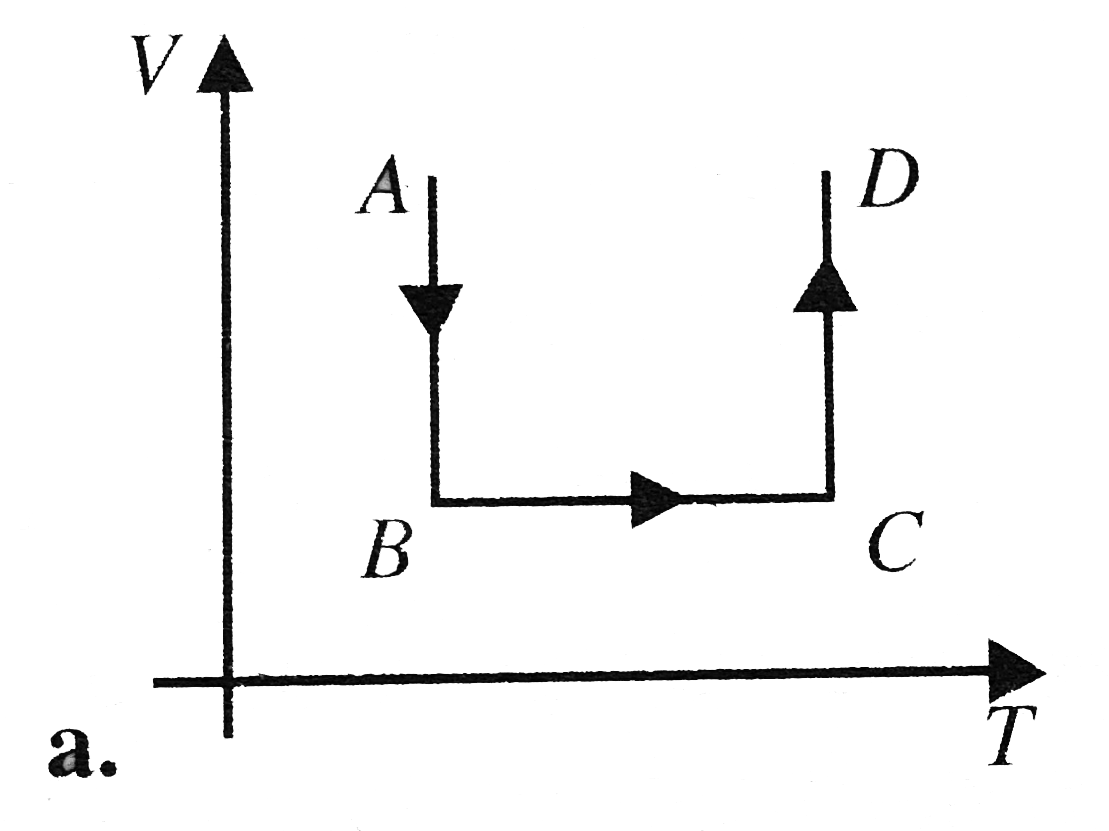 B
B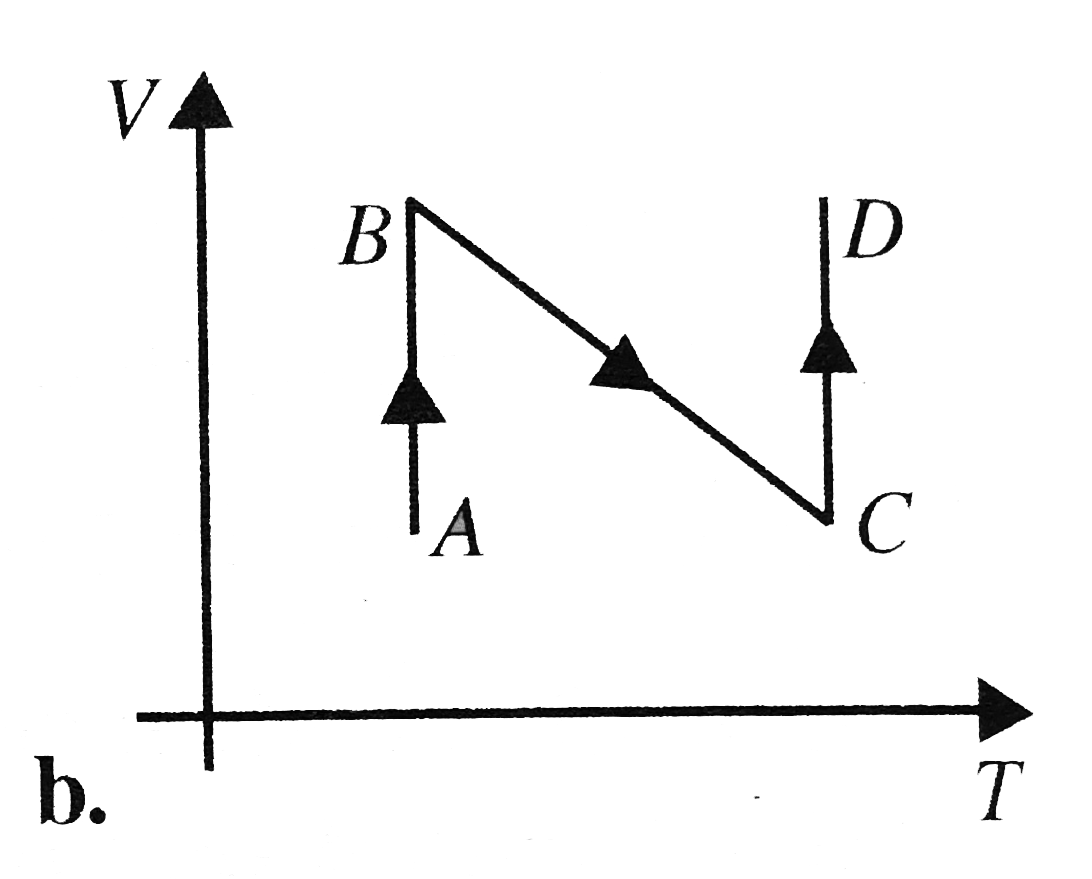 C
C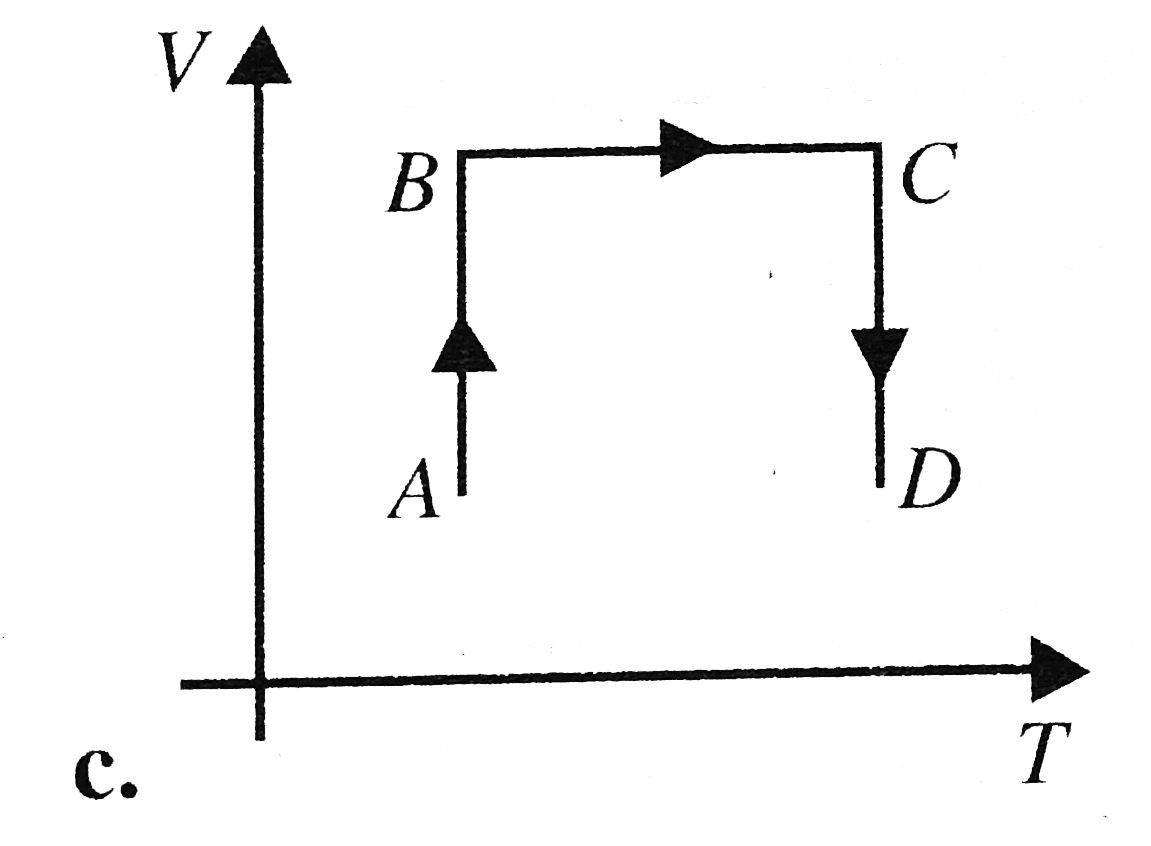 D
D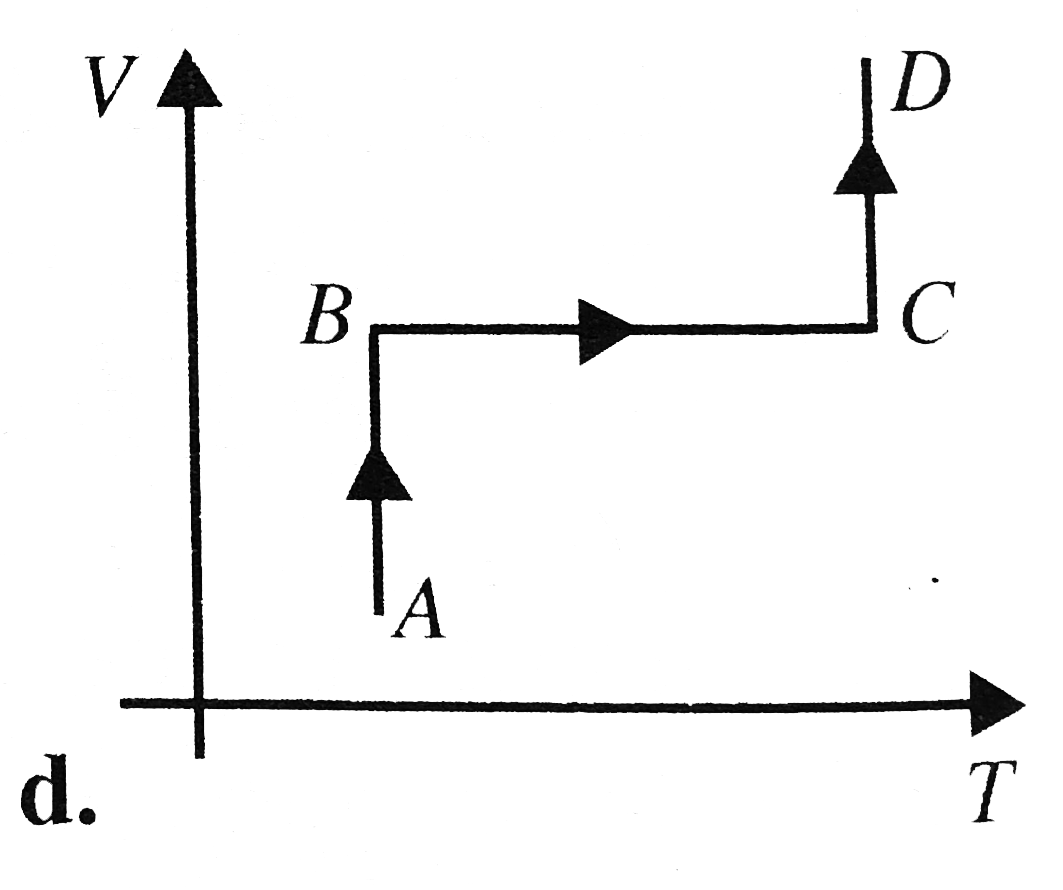
A planet orbits the sun in an elliptical path as shown in the figure. Let vp and vA be spped of the planet when at perohelion and aphelion respectively. Which of the following relations is correct ?
 ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvp
ArprA=vAvpBrprA=vpvACrprA=√vpvADrprA=√vAvpA planet is revolving around the sun. its distance from the sun at apogee is rA and that at perigee is rp. The masses of planet and sun are 'm' and M respectively, VA is the velocity of planet at apogee and VP is at perigee respectively and T is the time period of revolution of planet around the sun, then identify the wrong answer.
AT2=π2Gm(rA+rP)3BT2=π22GM(rA+rp)3CvArA=vPrPDvA<vP,rA>rp
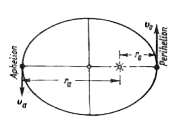
The point of an elliptical orbit closest to the Sun is called the perihelion, and the point most distant from it is called aphelion (Fig). Denoting the distance from the perihelion to the Sun by r0 and the velocity of the planet at the perihelion by v0 , find the radius of curvature of the orbit at the perihelion and at the aphelion, the distance from the aphelion to the Sun, and the velocity of the planet at the aphelion.
Prove that the motion of a planet in an elliptical orbit is only possible, if its total energy is negative.
View SolutionGiven the number of trms in ech of the expressions.
4 p p p r t u v
View SolutionThe relation between Ip and Vp for a triode is
Ip=(0.124Vp−7.5)mA
Keeping the grid potential constant at 1 V , the value of rp will be
View SolutionA planet goes round the sun three times as fast as the earth. If rpandre are the radii of orbit of the planet and the earth respectively then
View SolutionA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
View Solution
