A reflecting surface is represented by the equation
y=2Lπsin(πxL), where 0≤x≤L. A ray of light travelling horizontally becomes vertical after reflection with the surface. The co-ordinates of the point where this ray is incident is.
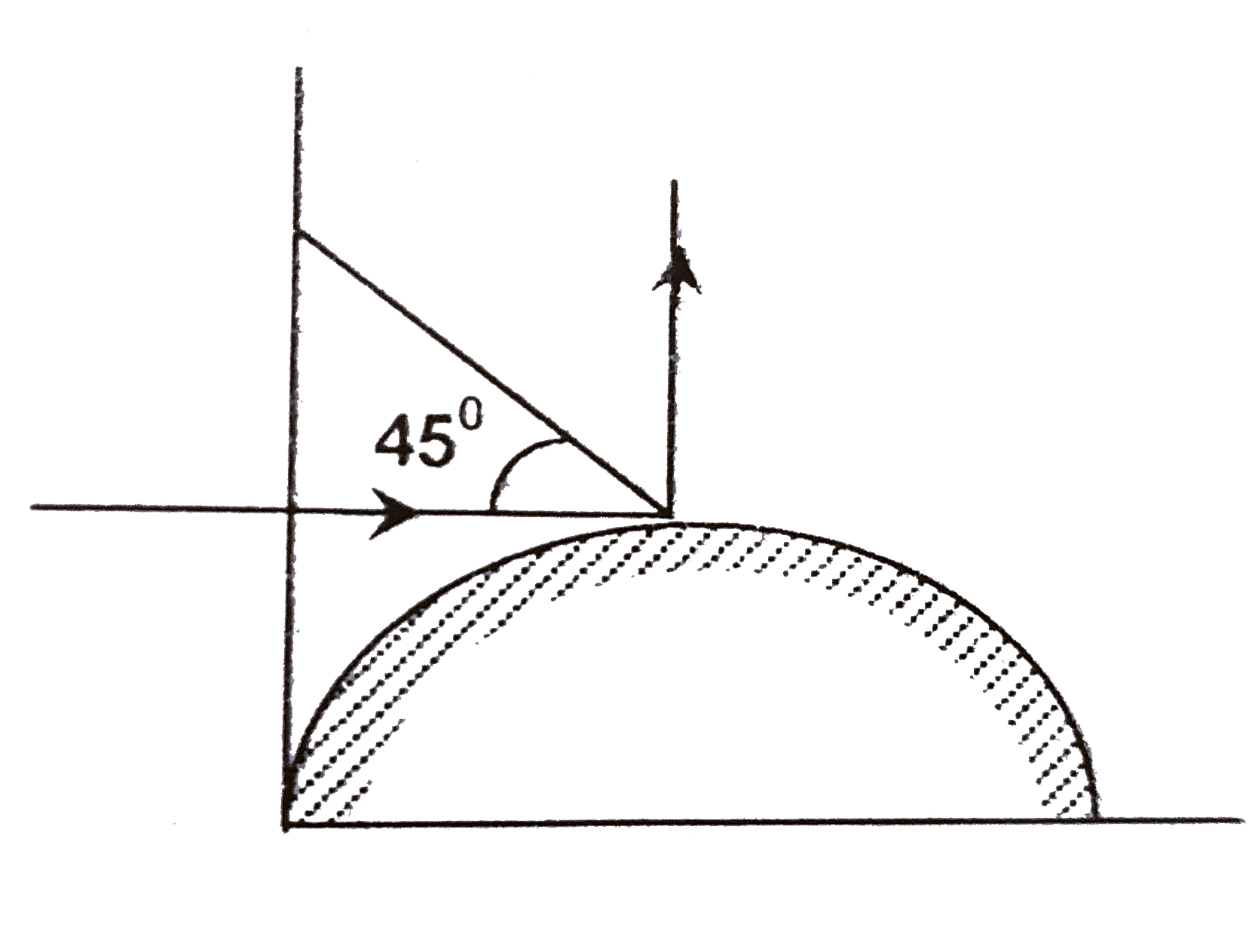
Ahorizontal ray becomes vertical after reflection.
tan θ=dydx=2cos(πx)L
2θ=90∘⇒θ⇒45∘
1 = 2 Cos (πx/2)
⇒L/3
∴ y = 2Lπsin(π3)=√3Lπ
(L3,√3Lπ)&(2L3,√3Lπ)

Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:CUQ (REFLECTION)
Explore 9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS Book:NARAYNAChapter:RAY OPTICS AND OPTICAL INSTRAUMENTS Exercise:CUQ (REFRECTION)
Explore 28 Videos
- NUCLEI Book:NARAYNAChapter:NUCLEI Exercise:ASSERTION & REASON
Explore 5 Videos
- SEMI CONDUCTOR DEVICESBook:NARAYNAChapter:SEMI CONDUCTOR DEVICESExercise:Level-II (H.W)
Explore 36 Videos
Similar Questions
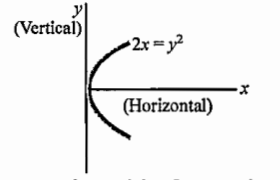
The reflecting surface is represented by the equation 2x=y2 as shown in the figure. A ray travelling horizontal becomes vertical after reflection. The co-ordinates of the point of incidence are
View SolutionA ray of light coming from origin after reflectiion at the point P(x,y) of any curve becomes parallel to x-axis, the , equation of the curve may be :
View Solution
Knowledge Check
A refracting surface is represented by the equation x2+y2=a2. A ray travelling in negative x-directed towards positive y-direction after reflection from the surface at point P. Then co-ordinates of point P are
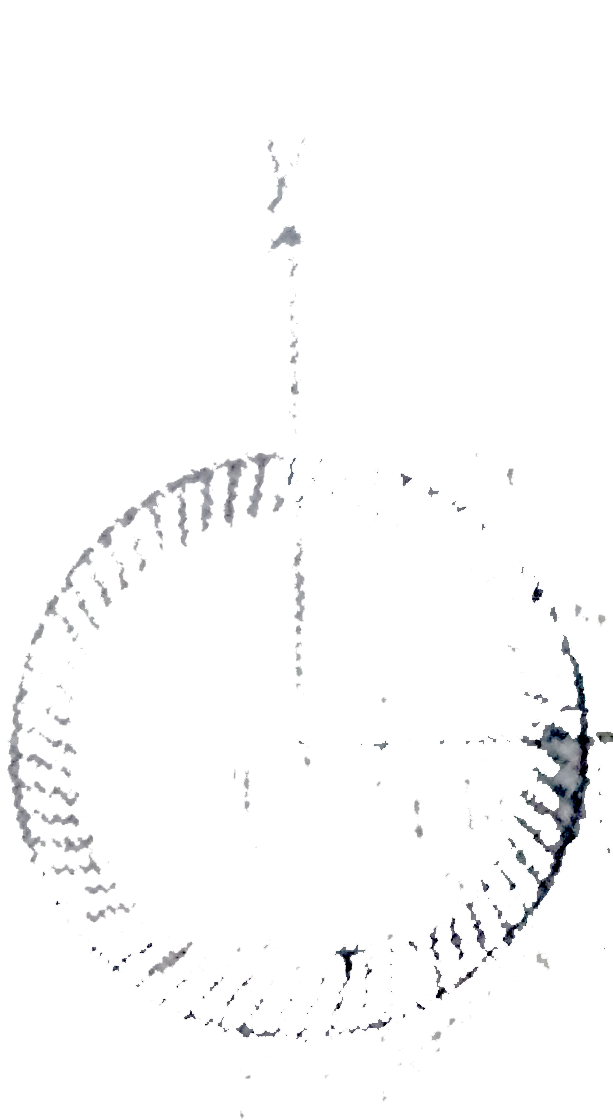 A(0.8 a, 0.6 a)B(0.6 a, 0.8 a)C(a2,a2)DNone of these
A(0.8 a, 0.6 a)B(0.6 a, 0.8 a)C(a2,a2)DNone of theseA wave is represented by the equation y=Asin(10πx+15πl+π6) wher x is in metre and t in second. The expression represents
AA wave travelling in negative x - direction with a velocity of 1.5 m/sBA wave travelling in positive x direction with a velocity of 1.5 m/sCA wave travelling in position x - direction with wavelength 0.2 mDA wave travelling in negative x-direction with a velocity of 150 m/sIf the equation of mirror is given by y=2/πsinπx(y>0,0≤x≤1) then find the point on which horizontal ray should be incident so that the reflected ray become perpendicular to the incident ray
_E01_073_Q01.png) A(13,√3π)B(√3π,13)C(23,√3π)D(1,0)
A(13,√3π)B(√3π,13)C(23,√3π)D(1,0)
A ray of light passing through the point (8,3) gets reflected after it meets x -axis at (14,0) .Then the equation of the reflected ray
View SolutionIf: sin(x+π6)=√32, where 0≤x≤2π, then: x=
View SolutionThe number of distinct real roots of the equation √sinx−1√sinx=cosx(where0≤x≤2π) is
View SolutionThe area bounded by the curves y=sin−1|sinx|andy=(sin−1|sinx|)2, where 0≤x≤2π, is
View SolutionA ray of light coming from the point (1,2) is reflected at a pont A on the x-axis and then passes through the point (5,3). The co ordinate of the point A is
View Solution