When an unknown resistance and a resistance of are connected in the left and right gaps of Meterbridge, the balance point is obtained at 50 cm. The shift in the balance point if 4 ohm resistance is connectedin parallel in the right gap is
66.7 cm
16.7 cm
34.6 cm
14.6 cm
The correct Answer is:B
To solve the problem step-by-step, we will use the principles of the meter bridge and the concept of parallel resistances.
Step 1: Understand the initial setup
We have an unknown resistance Rx and a known resistance of 4Ω connected in a meter bridge. The balance point is at 50cm.
Step 2: Apply the meter bridge formula
Using the meter bridge formula, we can write:
RxL=4100−L
Here, L=50cm and 100−L=50cm.
Step 3: Substitute the values into the equation
Substituting L into the equation:
Rx50=450
Step 4: Solve for the unknown resistance Rx
Cross-multiplying gives:
Rx⋅50=4⋅50
Rx=4Ω
Step 5: Analyze the new configuration
Now, we connect another 4Ω resistance in parallel with the existing 4Ω resistance in the right gap.
Step 6: Calculate the equivalent resistance of the parallel combination
The equivalent resistance Req of two resistances R1 and R2 in parallel is given by:
Req=R1⋅R2R1+R2
Substituting R1=4Ω and R2=4Ω:
Req=4⋅44+4=168=2Ω
Step 7: Set up the new balance point equation
Now, we will find the new balance point L′ using the new equivalent resistance:
RxL′=Req100−L′
Substituting Rx=4Ω and Req=2Ω:
4L′=2100−L′
Step 8: Cross-multiply to solve for L′
Cross-multiplying gives:
4(100−L′)=2L′
400−4L′=2L′
400=6L′
L′=4006=2003≈66.67cm
Step 9: Calculate the shift in the balance point
The initial balance point was at 50cm. The new balance point is 2003cm:
Shift=L′−L=2003−50=2003−1503=503≈16.67cm
Final Answer
The shift in the balance point is approximately 16.67cm.
---
We have an unknown resistance Rx and a known resistance of 4Ω connected in a meter bridge. The balance point is at 50cm.
Using the meter bridge formula, we can write:
RxL=4100−L
Here, L=50cm and 100−L=50cm.
Substituting L into the equation:
Rx50=450
Cross-multiplying gives:
Rx⋅50=4⋅50
Rx=4Ω
Now, we connect another 4Ω resistance in parallel with the existing 4Ω resistance in the right gap.
The equivalent resistance Req of two resistances R1 and R2 in parallel is given by:
Req=R1⋅R2R1+R2
Substituting R1=4Ω and R2=4Ω:
Req=4⋅44+4=168=2Ω
Now, we will find the new balance point L′ using the new equivalent resistance:
RxL′=Req100−L′
Substituting Rx=4Ω and Req=2Ω:
4L′=2100−L′
Cross-multiplying gives:
4(100−L′)=2L′
400−4L′=2L′
400=6L′
L′=4006=2003≈66.67cm
The initial balance point was at 50cm. The new balance point is 2003cm:
Shift=L′−L=2003−50=2003−1503=503≈16.67cm
The shift in the balance point is approximately 16.67cm.
Similar Questions
When two known resistance R and S are connected in the left and right gaps of a meter bridge, the balance point is found at a distance l1 from the zero end of the meter bridge wire. An unknown resistance X is now connected in parallel to the resistance S and the balance point is found at a distance l2 from the zero end of the meter bridge wire,
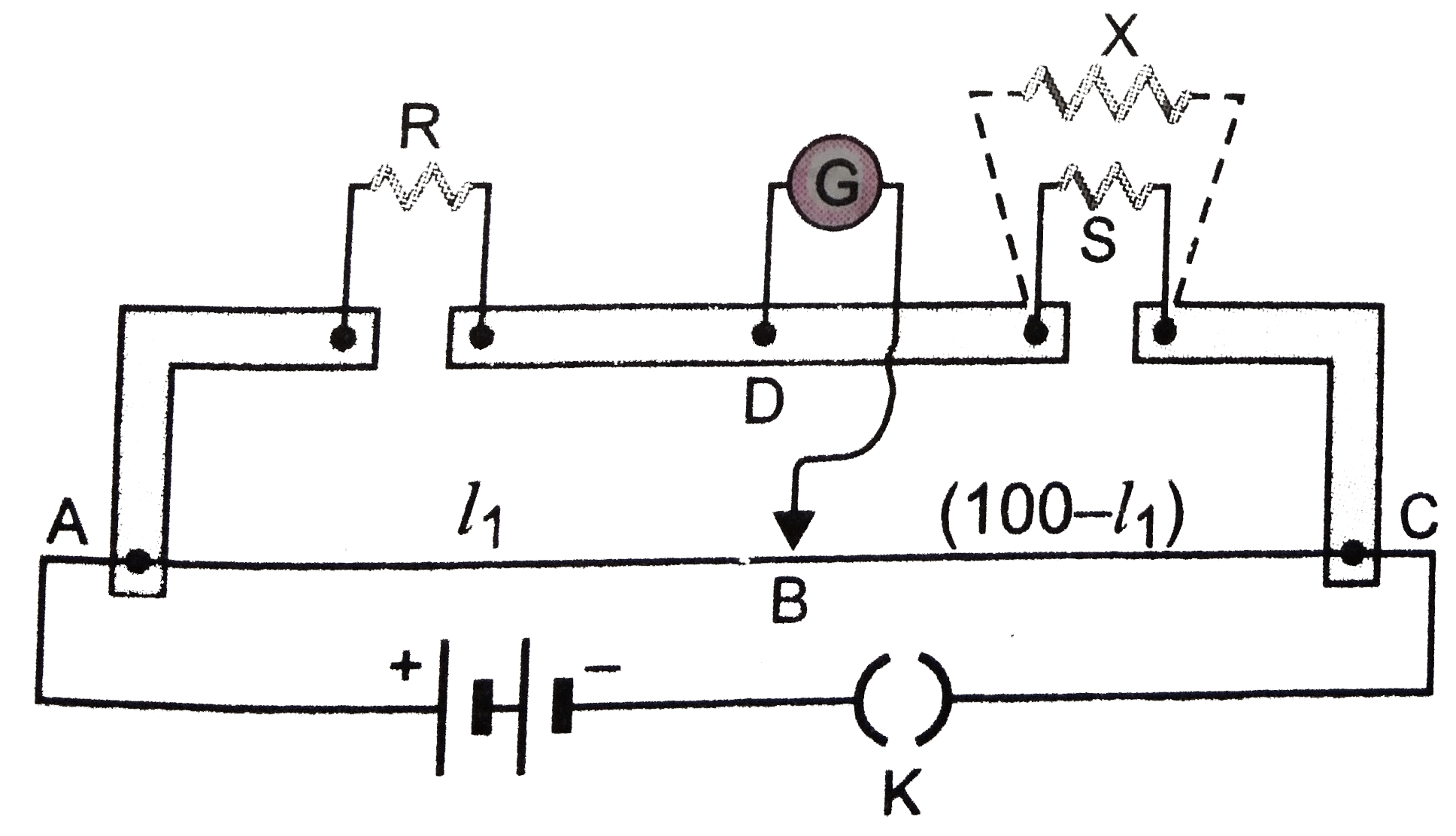
Obtain a formula for X in terms of l1,l2 and S.
View SolutionAn unknown resistance is placed in the left gap and resistance of 50 ohm is placed in the right gap of a meter bridge . The null point is obtained at 40 cm from the left end. Determine the unknown resistance.
View Solution
Knowledge Check
When an unknown resistance and a resistance of 4Ω are connected in the left and right gaps of a meterbridge, the balance point is obtained at 50 cm. the shift in the balance point if a 4Ω resistance is now connected in parallel to the resistance in the right gap is
A66.7 cmB16.7 cmC34.6 cmD14. 6 cmWhen an unknown resistance and a resistance 6Ω are connected in the left and right gaps of a meter bridge the balance point is obtained at 50 cm. if 3Ω resistance is connected in parallel to resistance in right gap, the balance point is
Adecreases by 25 cmBincreases by 25 cmCdecreases by 16.7 cmDincreases by 16.7 cmWhen unknown resistance and a resistance of 5Ω are used in left and rigt gaps of meter bridge the balance point is 50 cm. The balancing point of 5Ω resistance is now connected in seriece to the resistor in right gap
A20 cmB33.3 cmC60 cmD60 cm
With an unknown resistance X in the left gap and a resistance R in the right gap of a meter bridge, the neutral point is obtained at a distance of 75cm from the left end. The shift of null point if the unknown resistance is shunted by an equal resistance X and keeping same resistance in right gap is
View SolutionTwo unknown resistance X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80 cm from left. When a 10Ω resisance is connected in parallel to x, balance point is 50 cm from left. The values of X and Y respectively are
View SolutionIn a meter bridge experiment, null point is obtained at 20cm from one end of the wire when resistance X is balanced against another resistance Y. If X<Y, then the new position of the null point from the same end, if one decides to balance a resistance of 4X against Y will be at.
View SolutionIf the balance point is obtained at the 35th cm in a metre bridge the resistances in the left and right gaps are in the ratio of
View SolutionIn a metre bridge experiment, unknown resistance X and known resistance of 60Ω is connected in left and right gap of a metre bridge respectively. If the null point is obtained at 40 cm from the left end then the unknown resistance is
View Solution