Resistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged the balance point shifts by
33.3cm
66.67cm
25cm
50cm
The correct Answer is:D
To solve the problem step by step, we will analyze the situation of a meter bridge with two resistances and determine how the balance point shifts when the resistances are interchanged.
1. Understanding the Setup:
We have a meter bridge with two resistances, R1=10Ω and R2=30Ω. The bridge is balanced when the ratio of the resistances is equal to the ratio of the lengths on the bridge.
2. Setting Up the Balance Condition:
The balance condition for the meter bridge can be expressed as:
R1R2=L1100−L1
where L1 is the length from one end of the bridge to the balance point.
3. Substituting the Values:
Substituting R1=10Ω and R2=30Ω into the balance condition:
1030=L1100−L1
Simplifying the left side:
13=L1100−L1
4. Cross-Multiplying:
Cross-multiplying gives:
100−L1=3L1
5. Solving for L1:
Rearranging the equation:
100=4L1⟹L1=1004=25cm
6. Interchanging the Resistances:
Now, we interchange the resistances, so R1=30Ω and R2=10Ω. We set up the new balance condition:
R1R2=L2100−L2
Substituting the new values:
3010=L2100−L2
Simplifying:
3=L2100−L2
7. Cross-Multiplying Again:
Cross-multiplying gives:
100−L2=L23
8. Solving for L2:
Rearranging the equation:
300−3L2=L2⟹300=4L2⟹L2=3004=75cm
9. Calculating the Shift in Balance Point:
The shift in the balance point is calculated by finding the difference between the new and old balance points:
Shift=L2−L1=75cm−25cm=50cm
Final Answer:
The balance point shifts by 50 cm.
We have a meter bridge with two resistances, R1=10Ω and R2=30Ω. The bridge is balanced when the ratio of the resistances is equal to the ratio of the lengths on the bridge.
The balance condition for the meter bridge can be expressed as:
R1R2=L1100−L1
where L1 is the length from one end of the bridge to the balance point.
Substituting R1=10Ω and R2=30Ω into the balance condition:
1030=L1100−L1
Simplifying the left side:
13=L1100−L1
Cross-multiplying gives:
100−L1=3L1
Rearranging the equation:
100=4L1⟹L1=1004=25cm
Now, we interchange the resistances, so R1=30Ω and R2=10Ω. We set up the new balance condition:
R1R2=L2100−L2
Substituting the new values:
3010=L2100−L2
Simplifying:
3=L2100−L2
Cross-multiplying gives:
100−L2=L23
Rearranging the equation:
300−3L2=L2⟹300=4L2⟹L2=3004=75cm
The shift in the balance point is calculated by finding the difference between the new and old balance points:
Shift=L2−L1=75cm−25cm=50cm
The balance point shifts by 50 cm.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Heating Effect Of Current
40 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Problems Based On Mixed Concepts
34 Videos
- CURRENT ELECTRICITYBOOK - A2ZCHAPTER - CURRENT ELECTRICITYEXERCISE - Ammeter And Voltmeter
41 Videos
- ATOMIC PHYSICSBOOK - A2ZCHAPTER - ATOMIC PHYSICSEXERCISE - Section D - Chapter End Test
30 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
The balance point in a meter bridge is 45cm .If the resistances in the gaps are interchanged the new balance point is
View SolutionThe resistances in left and right gap of a meter brigdge are 20 ω and 30 ω respecitively when the resistance in the left gap is reduced to half its value then balance point shifts by
View Solution
Knowledge Check
Resistance in the two gaps of a meter bridge are 10ohm and 30ohm respectively. If the resistances are interchanged the balance point shifts by
A33.3cmB66.67cmC25cmD50cmThe resistances in the left and right gaps of a metre bridge are 10Ωand30Ω respectively. If the bridge is balanced, then the distance of the null point from the centre of the wire is
A20 cmB30 cmC40 cmD25 cmThe resistances in left and right gap of a meter brigdge are 20 ω and 30 ω respecitively when the resistance in the left gap is reduced to half its value then balance point shifts by
A15 cm to the rightB15 cm to the leftC20 cm to the rightD20 cm to the left
The resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is
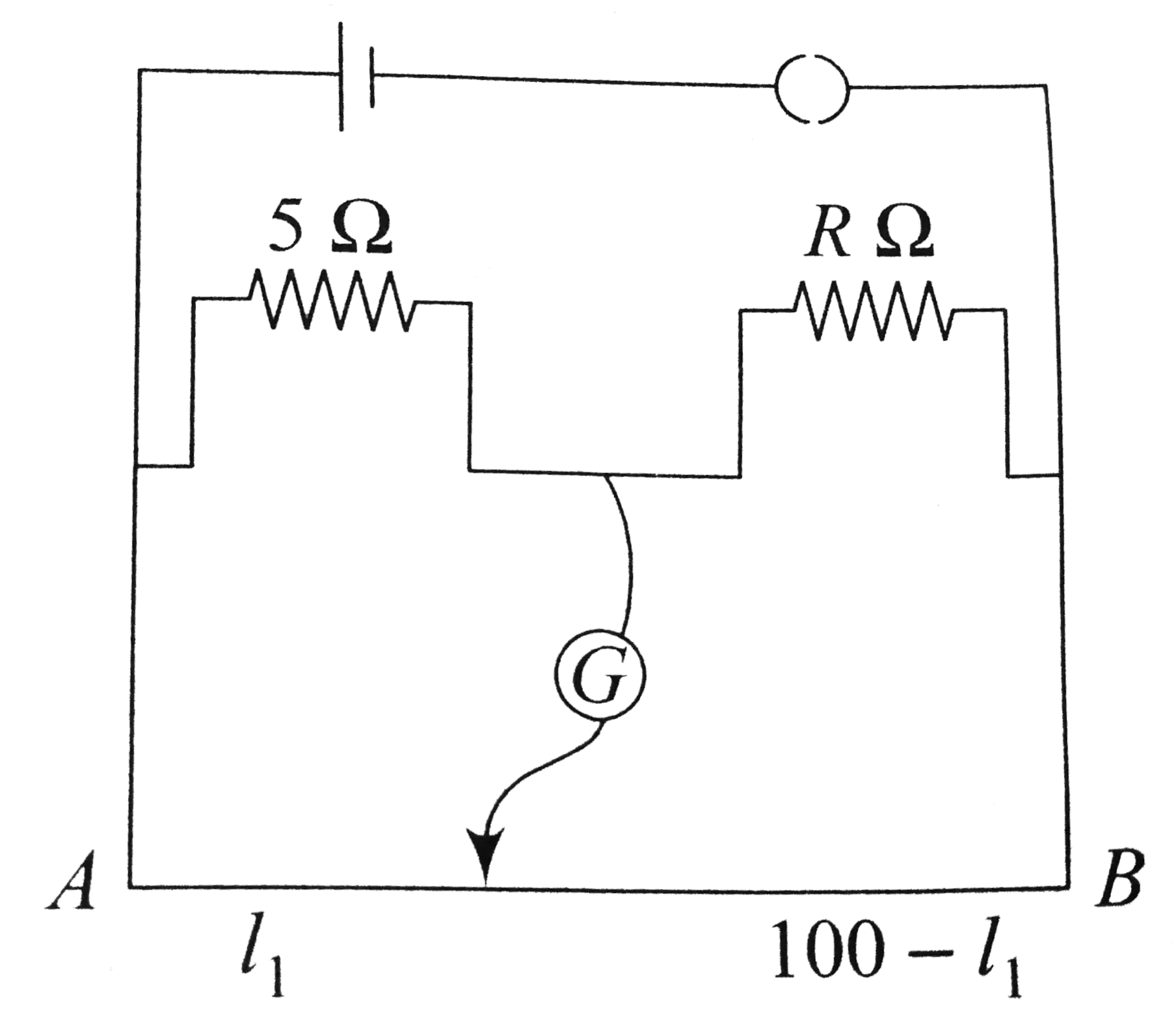
View SolutionThe resistance in the two arms of the meter bridge are 5Ω and RΩ, respectively. When the resistance R is shunted with an equal resistance, the new balance point is 1.6l1.
The resistance R is

View SolutionThe points in a metre bridge is at 35.6 cm. if the resistances in the gaps are interchanged, the new balance point is
View SolutionConsider a metre bridge whose length of wire is 2m. A resistance of 10Ω is connected across one gap of the meter bridge and an unknown resistance is connected across the other gap. When these resistances are interchanged, the balance point shifts by 50 cm. What is the value of the unknown resistance?
View SolutionA resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections, the unknown resistance is
View Solution
