A regular pentagon has four charges each +q at four of its vertices. At the centre of the pentagon, a charge +q is kept. If the distance of a vertex from the center is a the magnitude of the net force acting on the charge at the center is
q24pe0a2
zero
4q24pe0a2
2q24pe0a2
The correct Answer is:A
To solve the problem, we need to find the net force acting on a charge +q placed at the center of a regular pentagon with four other charges +q located at four of its vertices. The distance from the center to a vertex is given as 'a'.
1. Understanding the Configuration:
- We have a regular pentagon with vertices labeled A, B, C, D, and E.
- Charges +q are placed at vertices A, B, C, and D.
- A charge +q is placed at the center O of the pentagon.
- The distance from the center O to any vertex (A, B, C, or D) is 'a'.
2. Electric Field Due to One Charge:
- The electric field E due to a point charge +q at a distance a is given by:
E=k⋅qa2
where k is Coulomb's constant.
3. Direction of Electric Fields:
- The electric field at point O due to each of the charges at the vertices A, B, C, and D will point away from the charges since they are all positive.
- Due to the symmetry of the pentagon, the horizontal components of the electric fields from charges at A, B, C, and D will cancel out, while the vertical components will add up.
4. Calculating the Net Electric Field:
- The vertical components of the electric fields from the four charges can be calculated. Each charge contributes an electric field E at an angle of 72∘ (the angle between adjacent vertices of a pentagon).
- The vertical component of the electric field from one charge is:
Ey=E⋅sin(72∘)=k⋅qa2⋅sin(72∘)
- Since there are four charges, the total vertical component of the electric field at the center is:
Enet=4⋅Ey=4⋅k⋅qa2⋅sin(72∘)
5. Calculating the Net Force:
- The net force F acting on the charge at the center due to the electric field is given by:
F=Q⋅Enet=q⋅(4⋅k⋅qa2⋅sin(72∘))
- Simplifying this, we get:
F=4kq2sin(72∘)a2
6. Final Result:
- The magnitude of the net force acting on the charge at the center is:
F=4kq2sin(72∘)a2
- We have a regular pentagon with vertices labeled A, B, C, D, and E.
- Charges +q are placed at vertices A, B, C, and D.
- A charge +q is placed at the center O of the pentagon.
- The distance from the center O to any vertex (A, B, C, or D) is 'a'.
- The electric field E due to a point charge +q at a distance a is given by:
E=k⋅qa2
where k is Coulomb's constant.
- The electric field at point O due to each of the charges at the vertices A, B, C, and D will point away from the charges since they are all positive.
- Due to the symmetry of the pentagon, the horizontal components of the electric fields from charges at A, B, C, and D will cancel out, while the vertical components will add up.
- The vertical components of the electric fields from the four charges can be calculated. Each charge contributes an electric field E at an angle of 72∘ (the angle between adjacent vertices of a pentagon).
- The vertical component of the electric field from one charge is:
Ey=E⋅sin(72∘)=k⋅qa2⋅sin(72∘)
- Since there are four charges, the total vertical component of the electric field at the center is:
Enet=4⋅Ey=4⋅k⋅qa2⋅sin(72∘)
- The net force F acting on the charge at the center due to the electric field is given by:
F=Q⋅Enet=q⋅(4⋅k⋅qa2⋅sin(72∘))
- Simplifying this, we get:
F=4kq2sin(72∘)a2
- The magnitude of the net force acting on the charge at the center is:
F=4kq2sin(72∘)a2
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -3
Explore 50 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -4
Explore 43 Videos
- ELECTRIC CHARGES AND FIELDSBook:NARAYNAChapter:ELECTRIC CHARGES AND FIELDSExercise:EXERCISE -2 (C.W.)
Explore 39 Videos
- DUAL NATUREBook:NARAYNAChapter:DUAL NATUREExercise:LEVEL-II (H.W)
Explore 17 Videos
- ELECTRO MAGNETIC INDUCTIONBook:NARAYNAChapter:ELECTRO MAGNETIC INDUCTIONExercise:Level-II (H.W)
Explore 23 Videos
Similar Questions
A regular polygon has "20" sides.Equal charges,each "Q" ,are placed at "19" vertices of the polygon and a charge "q" is placed at the centre of polygon.If the distance of each vertex from the centre is 'a' net force experienced by "q" is -
View SolutionA regular hexagon of side 10 cm has a charge 5μC at each of its vertices. Calculate the potential at the center of the hexagon.
View Solution
Knowledge Check
Equal charges q are placed at the four corners A,B,C,Dof a square of length a. The magnitude of the force on the charge at B will be
A3q24πε0a2B4q24πε0a2C(1+2√22)q24πε0a2D(2+1√2)q24πε0a2Equal charges Q are placed at the four corners A, B, C, D of a square of length a. The magnitude of the force on the charge at B will be
A3Q24πε0a2B4Q24πε0a2C(1+1√22)Q24πε0a2D(2+1√2)Q24πε0a2A point charge +Q is placed at the centroid of an equilateral triangle. When a second charge +Q is placed at a vertex of the triangle, the magnitude of the electrostatic force on the central charge is 8 N. The magnitude of the net force on the central charge when a third charge +Q is placed at another vertex of the triangle is
AzeroB4NC4(√2)ND8N
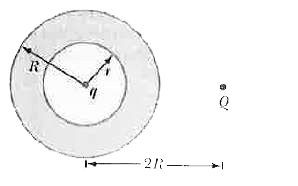
A conducting spherical shell of outer radius R and inner radius r = 3R/4 has no net charge on it. At its center there is a point charge q, and at a distance 2R from its center there is a point charge Q (Fig.) . (a) What is the magnitude of the electrostatic force on the charge q at the center due to the shell ? (b) What is the magnitude of net force on it?
View SolutionA charge Q exerts a 12 N force on another charge q. If the distance between the charges is doubled, what is the magnitude of the force exerted on Q by q?
View SolutionIn a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges of magnitude Q are placed at (n−1) corners. The field at the centre is
View SolutionA regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
View SolutionIn a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges each of magnitude q are placed at corners. The field at the centre is
View Solution

