A positively charged thin metal ring of radius R is fixed in the xy plane, with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
a. Periodic for all value of z0 satisfying 0<z0<∞ M
b. Simple harmonic, for all values of Z0 satisfying 0<z0≤R
c. Approximately simple harmonic, provided z0<<R
d. Such that P crosses O and continues to move along the negative z-axis towards z=−∞
Choose the correct answer
a and b are true
c is true
a,c,d are true
a,b,c,d are true
The correct Answer is:A
To solve the problem, we need to analyze the motion of a negatively charged particle P released from a point (0,0,z0) in the electric field created by a positively charged thin metal ring fixed in the xy-plane.
Step 1: Understanding the Electric Field
The electric field E due to a charged ring at a point along its axis (the z-axis) can be expressed as:
E=kQz(R2+z2)3/2
where:
- k is Coulomb's constant,
- Q is the total charge on the ring,
- R is the radius of the ring,
- z is the distance from the center of the ring along the z-axis.
Step 2: Analyzing the Force on the Particle
The force F acting on the negatively charged particle P is given by:
F=−qE
where q is the charge of particle P (which is negative). Therefore, the force acting on P will be directed towards the ring (the center), as the electric field points away from the positively charged ring.
Step 3: Motion of the Particle
Since the force is directed towards the center of the ring, the particle will experience a restoring force. This means that if the particle is displaced from its equilibrium position (the center of the ring), it will be pulled back towards that position.
Step 4: Conditions for Simple Harmonic Motion
For the motion to be classified as simple harmonic motion (SHM), the force must be directly proportional to the negative of the displacement:
F∝−z
This condition holds true when z (the distance from the center) is small compared to R (the radius of the ring).
Step 5: Evaluating the Options
- Option A: The motion is periodic for all values of z0 satisfying 0<z0<∞. This is true because the particle will always oscillate back and forth around the center.
- Option B: The motion is simple harmonic for all values of z0 satisfying 0<z0<R. This is not true, as SHM only occurs for small displacements.
- Option C: The motion is approximately simple harmonic provided z0≪R. This is true, as for small displacements, the force behaves like a restoring force.
- Option D: The particle crosses the origin and continues moving along the negative z-axis towards z=−∞. This is incorrect because the particle will oscillate back and forth rather than moving indefinitely in one direction.
Conclusion
The correct answers are A and C. The particle exhibits periodic motion for all values of z0 and approximately simple harmonic motion when z0 is much smaller than R.
The electric field E due to a charged ring at a point along its axis (the z-axis) can be expressed as:
E=kQz(R2+z2)3/2
where:
- k is Coulomb's constant,
- Q is the total charge on the ring,
- R is the radius of the ring,
- z is the distance from the center of the ring along the z-axis.
The force F acting on the negatively charged particle P is given by:
F=−qE
where q is the charge of particle P (which is negative). Therefore, the force acting on P will be directed towards the ring (the center), as the electric field points away from the positively charged ring.
Since the force is directed towards the center of the ring, the particle will experience a restoring force. This means that if the particle is displaced from its equilibrium position (the center of the ring), it will be pulled back towards that position.
For the motion to be classified as simple harmonic motion (SHM), the force must be directly proportional to the negative of the displacement:
F∝−z
This condition holds true when z (the distance from the center) is small compared to R (the radius of the ring).
- Option A: The motion is periodic for all values of z0 satisfying 0<z0<∞. This is true because the particle will always oscillate back and forth around the center.
- Option B: The motion is simple harmonic for all values of z0 satisfying 0<z0<R. This is not true, as SHM only occurs for small displacements.
The correct answers are A and C. The particle exhibits periodic motion for all values of z0 and approximately simple harmonic motion when z0 is much smaller than R.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -1 (C.W)
24 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EXERCISE -1 (H.W)
27 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EVALUATE YOURSELF-4
6 Videos
- DUAL NATUREBOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)
17 Videos
- ELECTRO MAGNETIC INDUCTIONBOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)
23 Videos
Similar Questions
Knowledge Check
A circular ring carries a uniformly distributed positive charge and lies in the xy plane with center at the origin of the cooredinate system. If at a point (0,0,z) the electric field is E, then which of the following graphs is correct?
A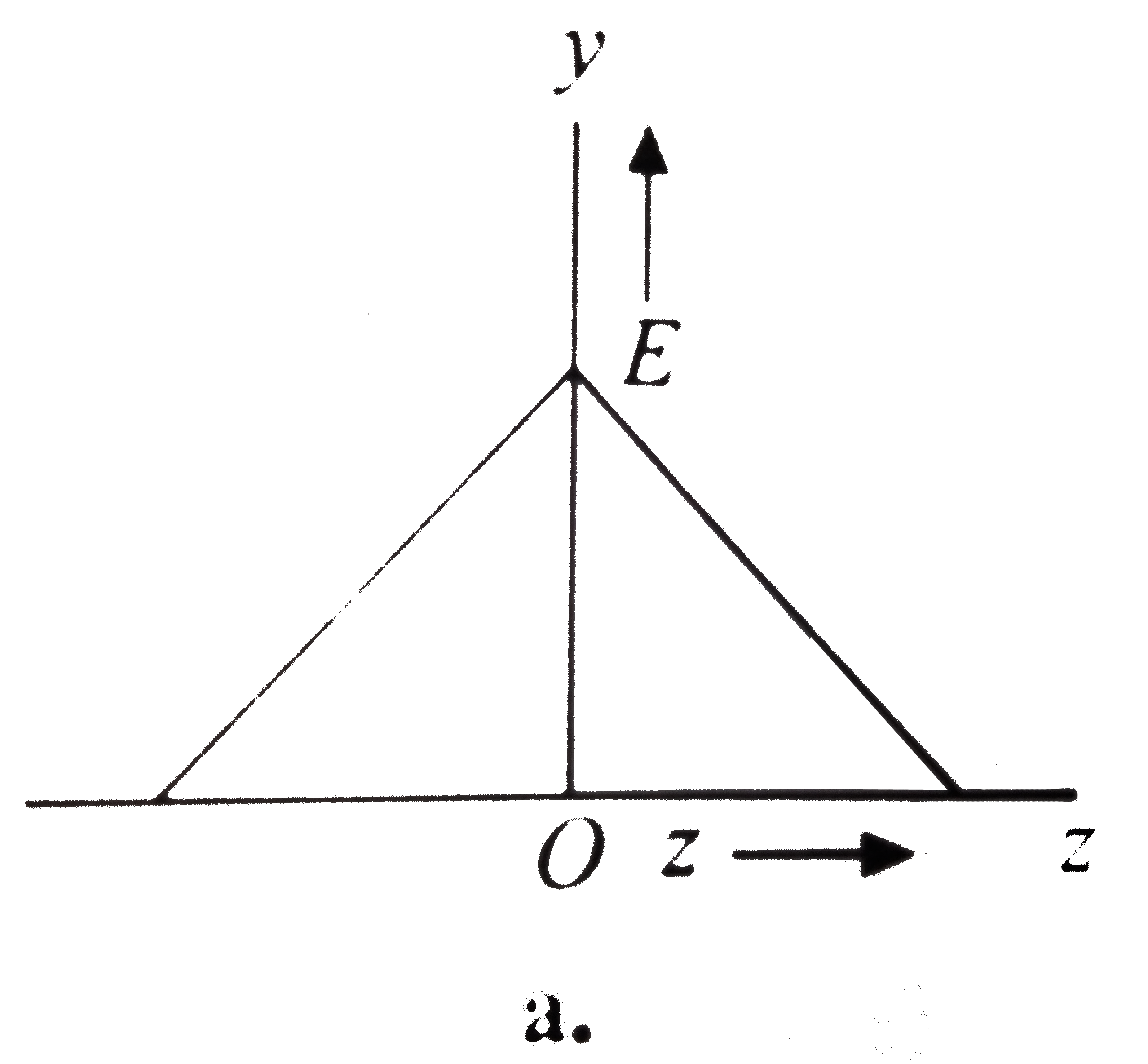 B
B C
C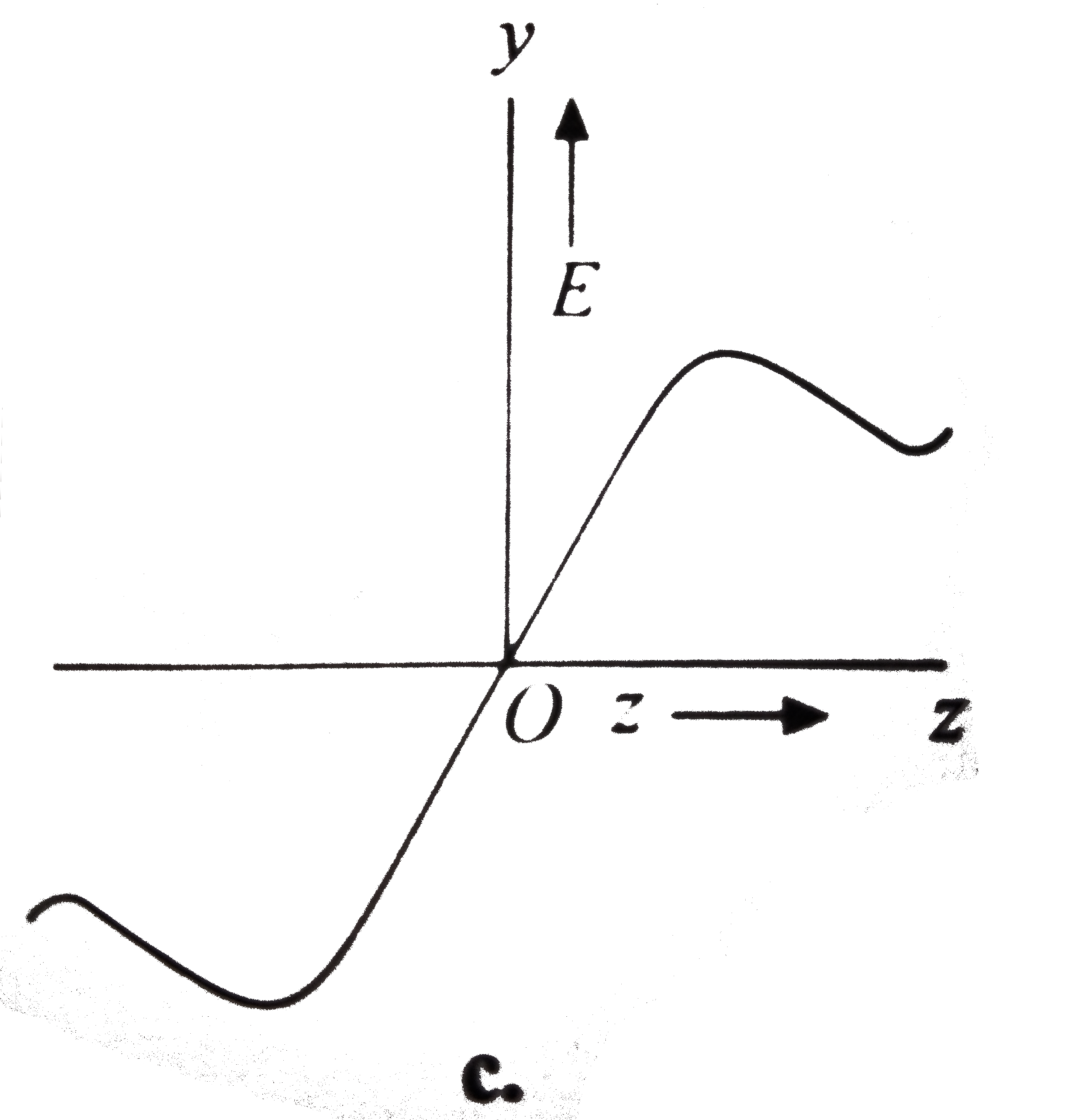 D
D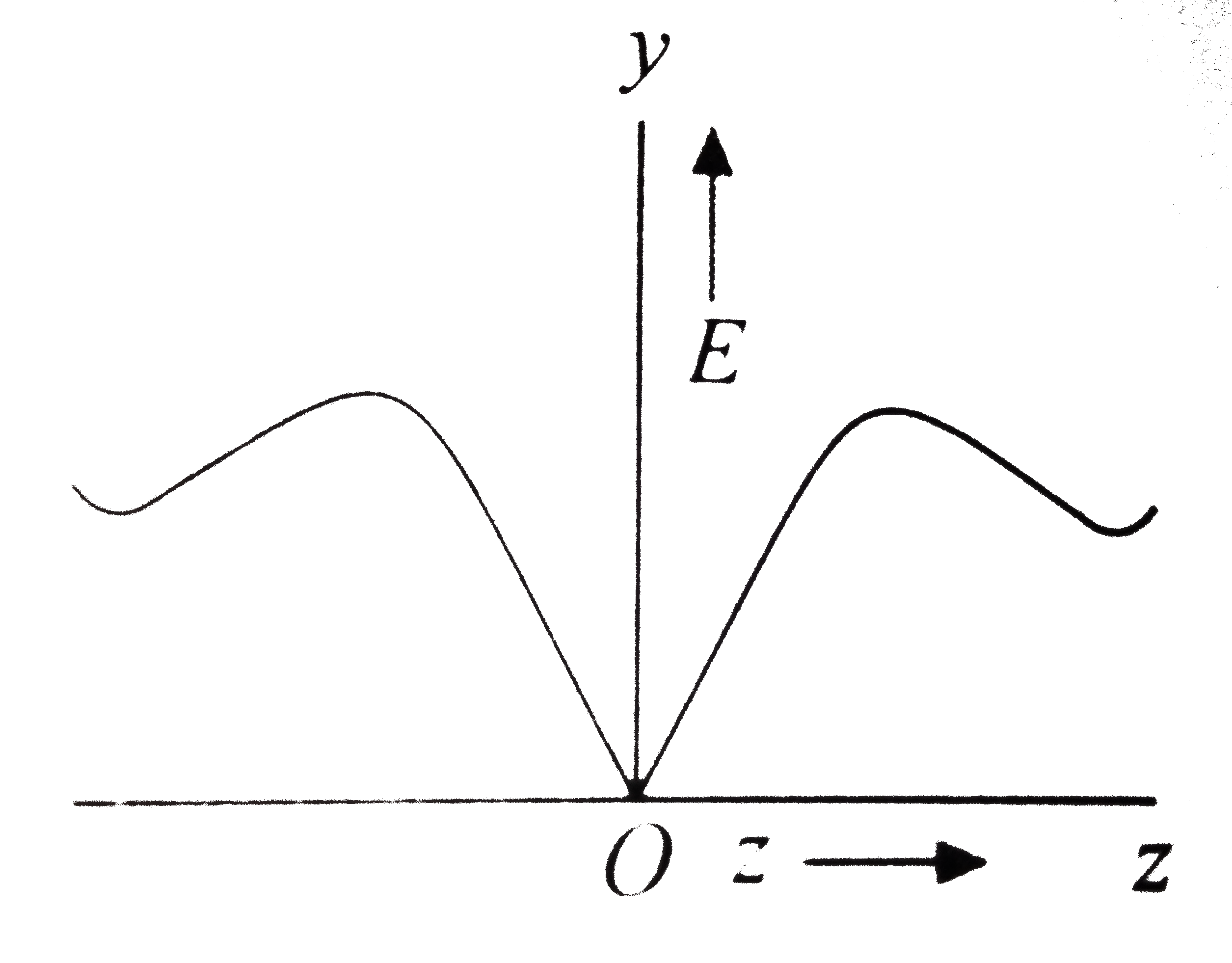
The locus of point z satisfying Re(z2)=0, is
Aa pair of straight linesBa circleCa rectangular hyperbolaDnone of theseIf z is a complex number satisfying |z|2−|z|−2<0, then the value of ∣∣z2+zsinθ∣∣, for all values of θ, is
Aequal to 4Bequal to 6Cmore than 6Dless than 6
calculate the electric potential at point (15cm, 0, 0) if the ring is placed parallel to y-z plane with centre at the origin and metallic ring with charge 0.02 μC made from a wire of length 12 cm.
View Solutionperpendicular distance of the point (0,0,0) from the plane 2x−3y+6z+14=0
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y z plane with its center at the origin O. A particle of mass m and positive charge q is projected from that point p(−√3R,0,0) on the negative x - axis directly toward O, with initial speed V. Find the smallest (nonzero) value of the speed such that the particle does not return to P ?
View SolutionA circular ring of radius R with uniform positive charge density λ per unit length is located in the y-z plane with its centre at the origin O. A particle of mass m and positive charge q is projected from the point P (R√3,0,0) on the positive x-axis directly towards O, with an initial speed v. Find the smallest (non-zero) value of the speed v such that the particle does not return to P.
View SolutionIf P=(0,1,0)andQ=(0,0,1) then the projection of PQ on the plane x+y+z=3 is
View Solution
