calculate the electric potential at point (15cm, 0, 0) if the ring is placed parallel to y-z plane with centre at the origin and metallic ring with charge 0.02 μC made from a wire of length 12 cm.
To calculate the electric potential at the point (15 cm, 0, 0) due to a metallic ring with charge, we can follow these steps:
Step 1: Identify the parameters
- The charge Q on the ring is given as 0.02μC=0.02×10−6C.
- The radius R of the ring can be calculated from its length. The length of the wire used to make the ring is 12cm=0.12m. Since the ring is circular, we can find the radius using the formula for the circumference of a circle:
L=2πR⟹R=L2π=0.122π≈0.0191m
Step 2: Calculate the distance from the point to the ring
The point where we want to calculate the potential is at (15 cm, 0, 0) or (0.15 m, 0, 0). The distance r from the point to the ring can be calculated using the Pythagorean theorem:
r=√x2+R2
where x=0.15m and R=0.0191m:
r=√(0.15)2+(0.0191)2=√0.0225+0.00036481≈√0.02286481≈0.151m
Step 3: Calculate the electric potential V
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant, approximately 8.99×109N⋅m2/C2. Substituting the values:
V=(8.99×109)×(0.02×10−6)0.151
Calculating this gives:
V≈(8.99×109)×(0.02×10−6)0.151≈1.798×1030.151≈1191.39V
Final Answer
The electric potential at the point (15 cm, 0, 0) is approximately 1191.39 V.
---
- The charge Q on the ring is given as 0.02μC=0.02×10−6C.
- The radius R of the ring can be calculated from its length. The length of the wire used to make the ring is 12cm=0.12m. Since the ring is circular, we can find the radius using the formula for the circumference of a circle:
L=2πR⟹R=L2π=0.122π≈0.0191m
The point where we want to calculate the potential is at (15 cm, 0, 0) or (0.15 m, 0, 0). The distance r from the point to the ring can be calculated using the Pythagorean theorem:
r=√x2+R2
where x=0.15m and R=0.0191m:
r=√(0.15)2+(0.0191)2=√0.0225+0.00036481≈√0.02286481≈0.151m
The electric potential V at a distance r from a point charge Q is given by the formula:
V=kQr
where k is Coulomb's constant, approximately 8.99×109N⋅m2/C2. Substituting the values:
V=(8.99×109)×(0.02×10−6)0.151
Calculating this gives:
V≈(8.99×109)×(0.02×10−6)0.151≈1.798×1030.151≈1191.39V
The electric potential at the point (15 cm, 0, 0) is approximately 1191.39 V.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 4
7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 5
18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 2
21 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
Knowledge Check
The electric field at point (30, 30, 0) due to a charge 0.008μC at origin will be (coordinates are in cm)
A8000NC−1B4000(ˆi+ˆj)NC−1C200√2(ˆi+ˆj)NC−1D400√2(ˆi+ˆj)NC−1The magnetic induction at the centre of a coil made from a wire of length 22 cm carrying a current of 0.5 A is
A8×10−6Wb/m2B0.9×10−6Wb/m2C9×10−6Wb/mD0.8×10−6Wb/m2A point P (R√3m,0,) lies on the axis of a ring of mass M and radius R. The ring is located in y−z plane with its centre at origin. A small particle of mass m start from P and reaches O under gravitational attraction only. Its speed at O will be.
A√GMRB√GmRC√GM√2RD√Gm√2R
A thin wire carrying current i is bent to form a closed loop of one turn. The loop is placed in y-z plane with centre at origin. If R is the radius of the loop, then
View SolutionA circular coil with 100 turns and radius 20 cm is kept in Y-Z plane with its centre at the origin. Find the magnetic field at point (20 cm, 0, 0) if coil carries a current of2.0 A.
View SolutionA plane passes through thee points P(4,0,0)andQ(0,0,4) and is parallel to the Y-axis. The distance of the plane from the origin is
View SolutionA uniform semicircular ring of radius R is in yz plane with its centre at the origin. The half ring carries a uniform linear charge density of λ.
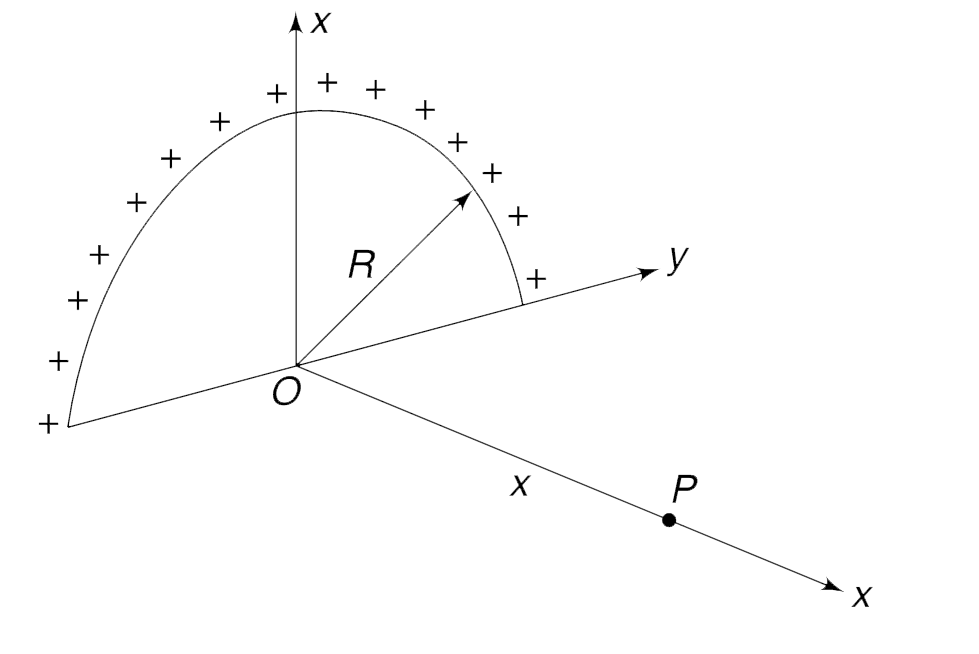
(a) Find the x, y and z component of Electric field at a point P(x, 0, 0) on the axis of the ring. (b) Prove that the field at P is directed along a line joining the centre of mass of the half ring to the point P.
View SolutionA positively charged thin metal ring of radius R is fixed in the xy plane with its centre at the origin O. A negatively charged particle P is released from rest at the point (0,0,z0) where z0>0. Then the motion of P is
View Solution