Calculate the electric potential at the centre of a metallic ring with charge 0.02 μC made from a wire of length 12 cm.
To calculate the electric potential at the center of a metallic ring with a charge of 0.02 µC and a wire length of 12 cm, we can follow these steps:
Step 1: Determine the radius of the ring
The length of the wire that forms the ring is equal to the circumference of the ring. The circumference C of a circle is given by the formula:
C=2πr
where r is the radius. Given that the length of the wire is 12 cm, we can set up the equation:
2πr=12 cm
To find r, we rearrange the equation:
r=122π=6π cm
Step 2: Convert the radius to meters
Since we will be using SI units, we need to convert the radius from centimeters to meters:
r=6π cm=6π×100 m=6314.16 m≈0.0191 m
Step 3: Use the formula for electric potential
The electric potential V at the center of a metallic ring is given by the formula:
V=kQr
where:
- k is Coulomb's constant, approximately 9×109N m2/C2
- Q is the charge in coulombs
- r is the radius in meters
Given that the charge Q=0.02μC=0.02×10−6C=2×10−8C, we can substitute the values into the formula.
Step 4: Substitute the values into the formula
Now we can substitute the values of k, Q, and r into the potential formula:
V=9×109×2×10−80.0191
Step 5: Calculate the potential
Now we perform the calculation:
V=9×109×2×10−80.0191≈1.8×1020.0191≈9423.5V
Thus, the electric potential at the center of the metallic ring is approximately:
V≈9.42×103V
Final Answer:
The electric potential at the center of the metallic ring is approximately 9.42 kV.
---
The length of the wire that forms the ring is equal to the circumference of the ring. The circumference C of a circle is given by the formula:
C=2πr
where r is the radius. Given that the length of the wire is 12 cm, we can set up the equation:
2πr=12 cm
To find r, we rearrange the equation:
r=122π=6π cm
Since we will be using SI units, we need to convert the radius from centimeters to meters:
r=6π cm=6π×100 m=6314.16 m≈0.0191 m
The electric potential V at the center of a metallic ring is given by the formula:
V=kQr
where:
- k is Coulomb's constant, approximately 9×109N m2/C2
- Q is the charge in coulombs
- r is the radius in meters
Now we can substitute the values of k, Q, and r into the potential formula:
V=9×109×2×10−80.0191
Now we perform the calculation:
V=9×109×2×10−80.0191≈1.8×1020.0191≈9423.5V
V≈9.42×103V
The electric potential at the center of the metallic ring is approximately 9.42 kV.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 4
Explore 7 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 5
Explore 18 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:MODERN PUBLICATIONChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:PRACTICE PROBLEMS 2
Explore 21 Videos
- ELECTROMAGNETIC WAVESBook:MODERN PUBLICATIONChapter:ELECTROMAGNETIC WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
- MAGNETISM AND MATTERBook:MODERN PUBLICATIONChapter:MAGNETISM AND MATTERExercise:CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
Explore 16 Videos
Similar Questions
calculate the electric potential at point (15cm, 0, 0) if the ring is placed parallel to y-z plane with centre at the origin and metallic ring with charge 0.02 μC made from a wire of length 12 cm.
View SolutionCalculate the electric field at the centre of a cube, if seven of its corners are given a charge of 0.02 μC and side of cube is 10 mm.
View Solution
Knowledge Check
The electric potential at the centre of a charged conductor is
AzeroBtwice that of the surfaceCsame as on the surfaceDnone of theseThe electric field at the centre of a uniformly charged ring is zero. What is the electric field and potential at the centre of a half ring if the charge on it be Q and its radius be R?
A14πε0QπR2,14πε0QπRB14πε0QR2,14πε02QπRC14πε02QπR2,14πε0QRD14πε02QR2,14πε03QπRThe magnetic induction at the centre of a coil made from a wire of length 22 cm carrying a current of 0.5 A is
A8×10−6Wb/m2B0.9×10−6Wb/m2C9×10−6Wb/mD0.8×10−6Wb/m2
Calculate the electric potential at the center of a square of side √2m, having charges 100μc,−50μC,20μcand−60μC at the four corners of the square.
View SolutionCalculate the potential at point (0, 7 cm) due to a point charge of 0.2 μC placed at (0, 2 cm).
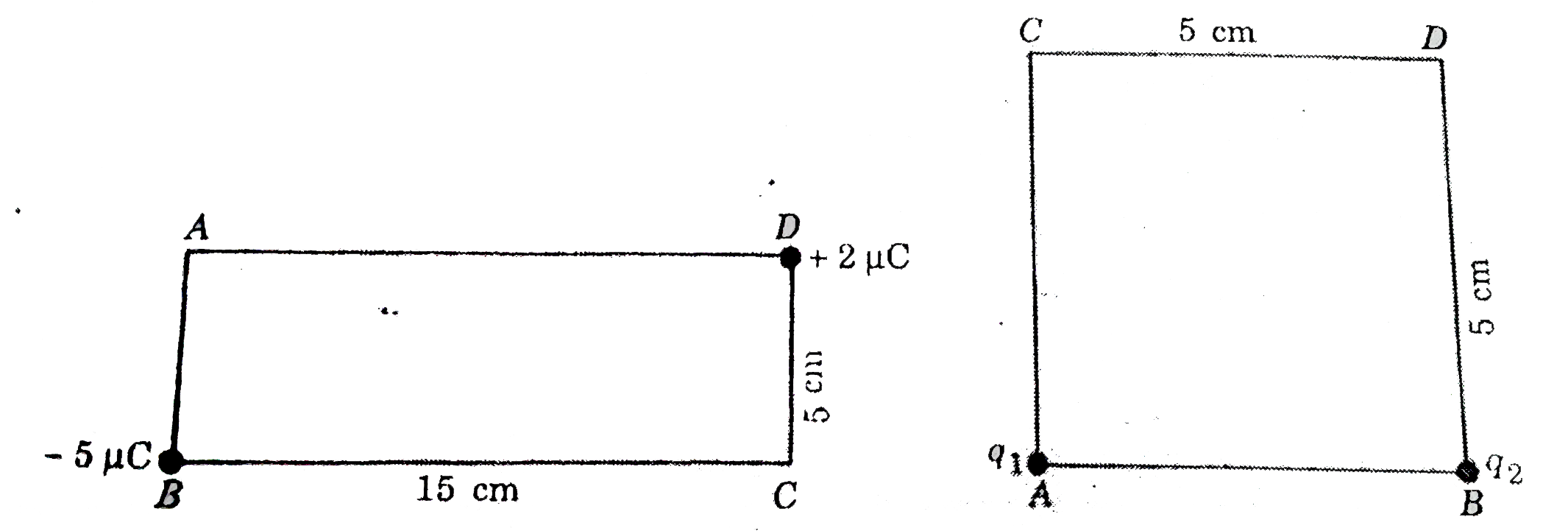
View SolutionThe sides of rectangle ABCD are 15 cm and 5 cm, as shown in figure. Point cahrges of −5μC and +2μC are placed at the vertices B and D respectively. Calculate electric potential at the vertices A and C. Also calculate the work done in carrying a charge of 3μC from A to C.
View SolutionCalculate the electric field intensity due to an electric dipole of length 10 cm having charges of 100μC at a point 20 cm from each charge on equatorial line.
View SolutionA charge of 108 μC is given to a metallic spherical shell of radius1 m. (i) Calculate electric potential at the surface of the shell. (ii) Calculate electric potential at a point that is 0.1 m from the centre of the shell.
View Solution

