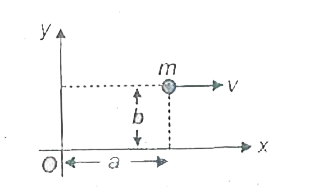
A particle moving parallel to x-axis as shown in fig. such that at all instant the y-axis component of its position vector is constant and is equal to 'b'. Find the angular velocity of the particle about the origin when its radius vector makes angle θ from the axis.
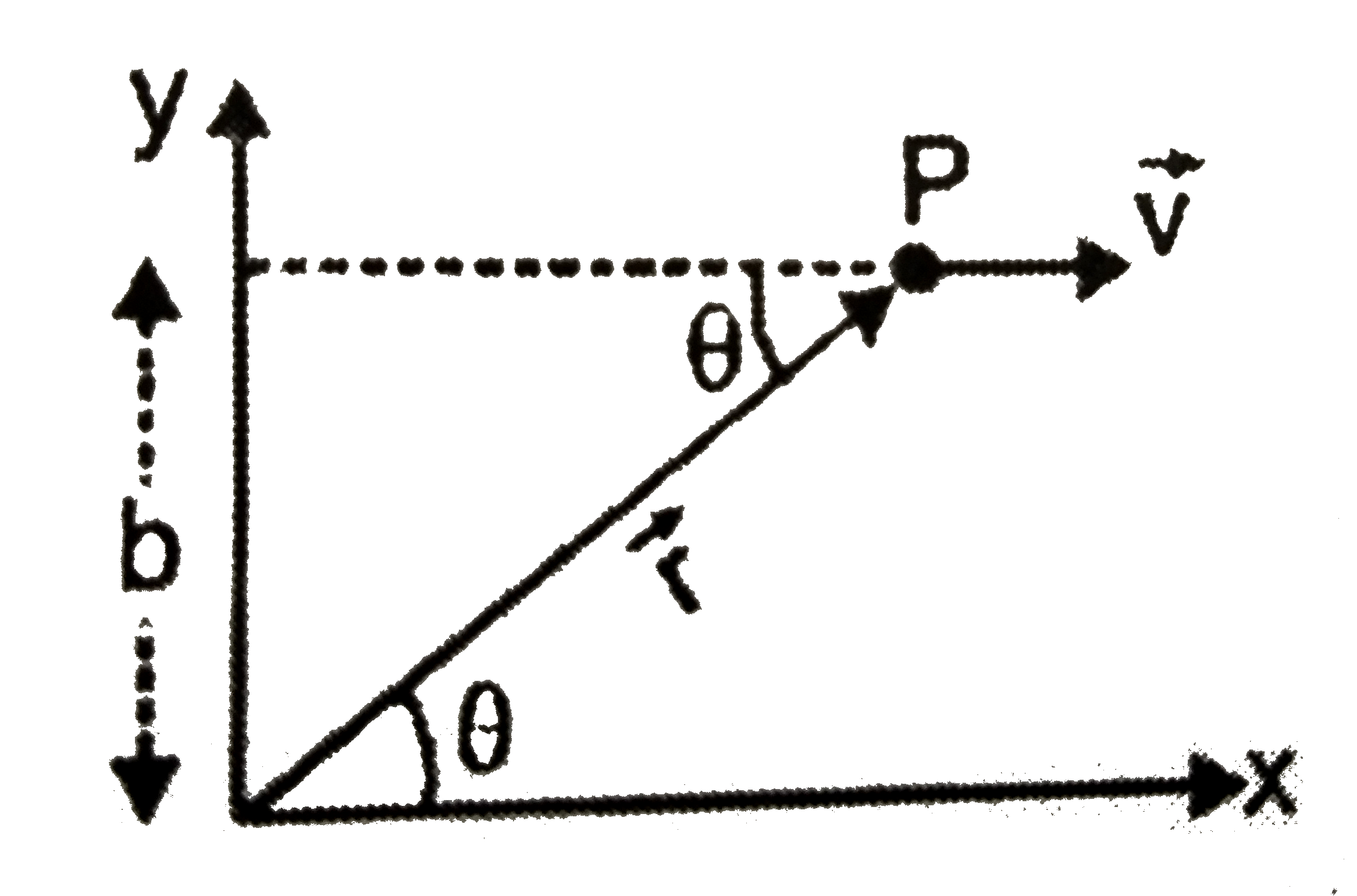
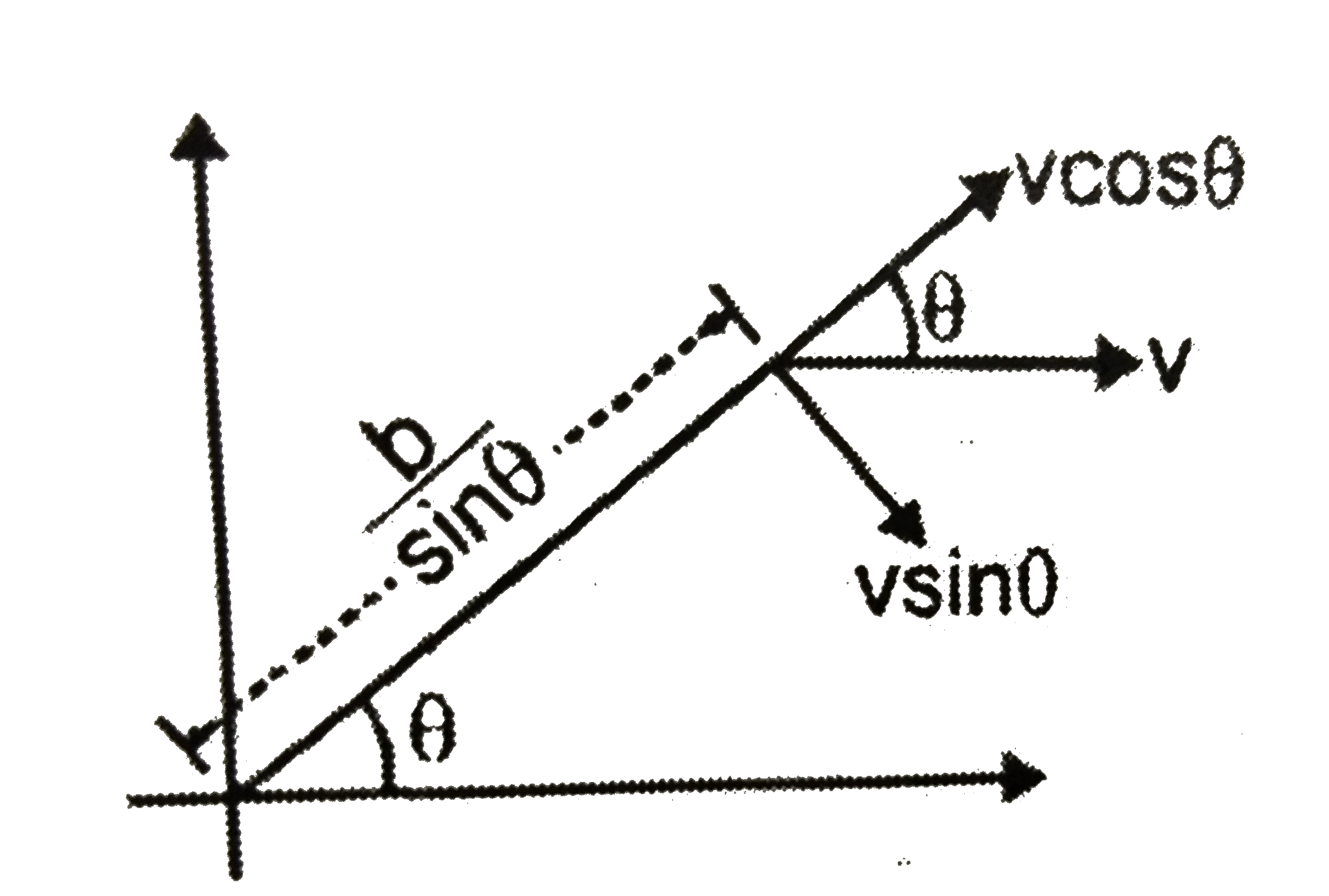
∴ωPO=vsinθbsinθ=vbsin2θ
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (S-1)
10 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - Dynamics of circular motion
8 Videos
- BASIC MATHSBOOK - ALLENCHAPTER - BASIC MATHSEXERCISE - Question
1 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
Similar Questions
A particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle is going parallel to x - axis with constant speed V at a distance 'a' from the axis . Find its angular velocity about an axis passing the origin O , at the instant when radial vector of the particle makes angle θ with the x - axis
View Solution
Knowledge Check
A particle moves parallel to X-axis as shown in the figure such that at all instant the y axis component of its position vector is constant and is equal to 'b'. The angular velocity of the particle about the origin is
 AvbBvbsinθCvbsin2θDvb
AvbBvbsinθCvbsin2θDvbA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
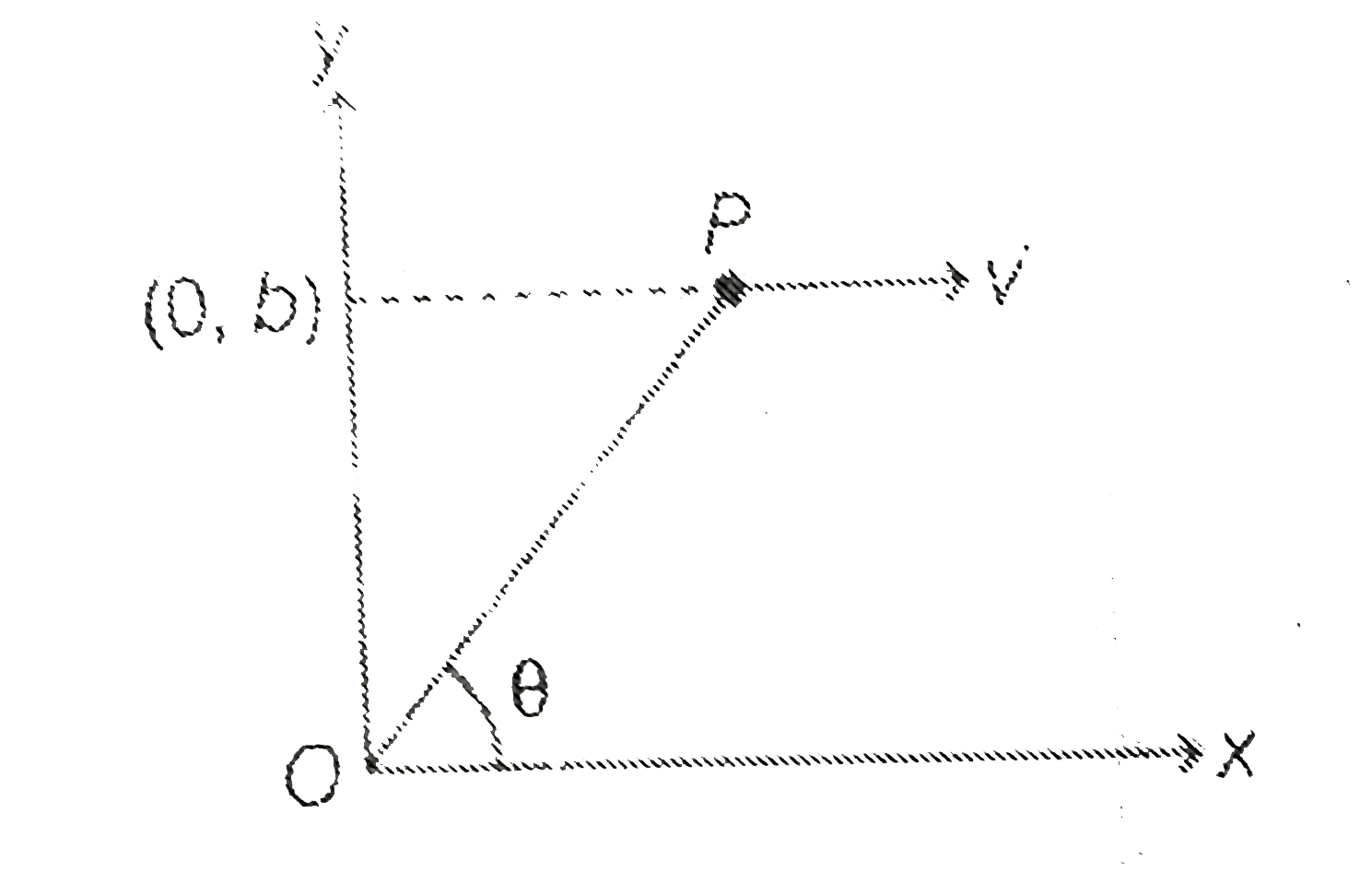 A(v/b)sin2θB(v/b)C(v/b)sinθDvbsinθ
A(v/b)sin2θB(v/b)C(v/b)sinθDvbsinθ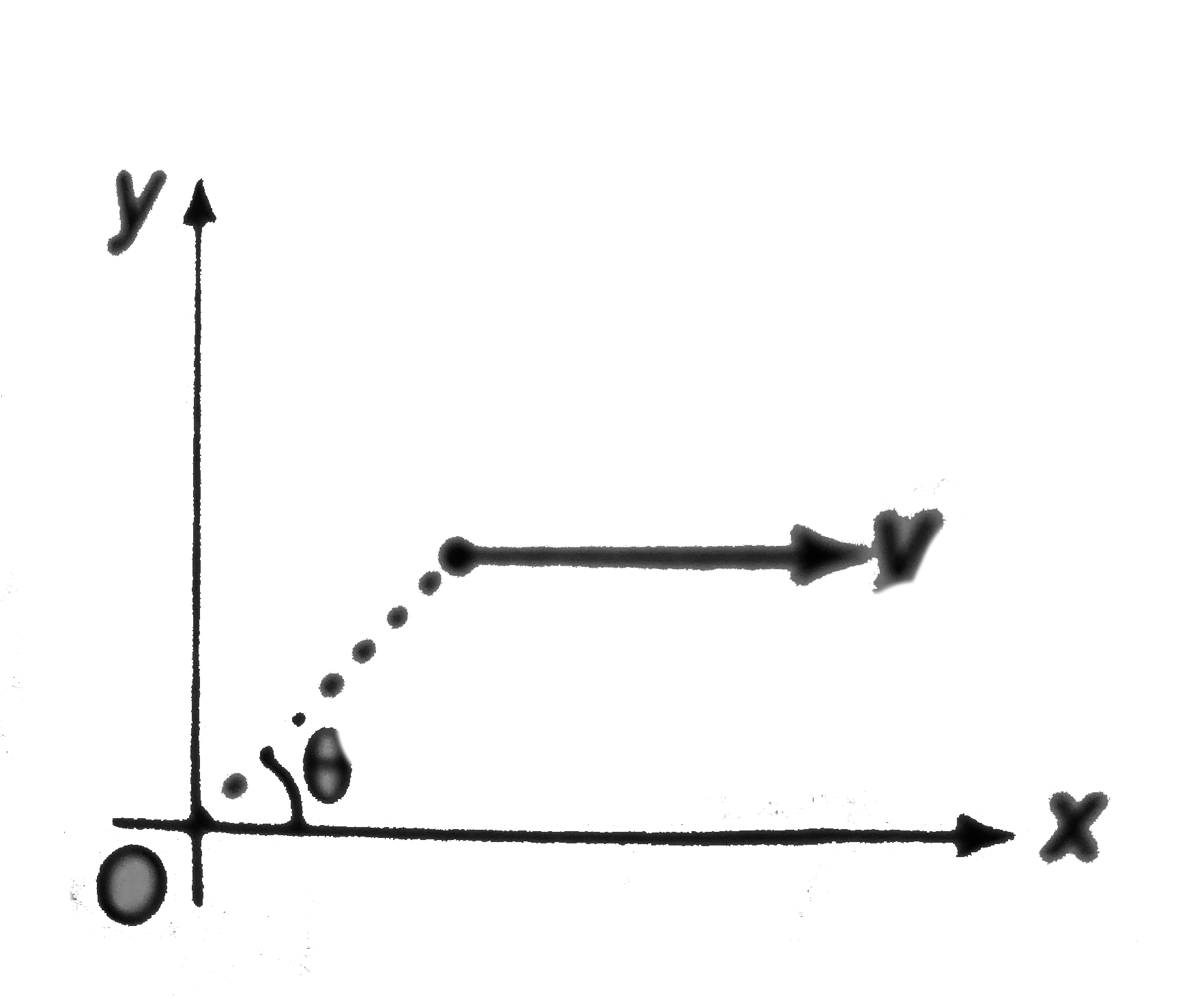
A particle mass parallel to x-axis with constant velocity v as shown in the figure. The angular velocity of the particle about the origin OAremains constantBcontinuously increasesCcontinuously decreasesDoscillates.
A particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

View SolutionA particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
View SolutionA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
View SolutionA circular of radius 20 cm is rotating about its own axis at an angular velocity ω . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
View Solution
