A particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle θ with x-axis.
vsin2θa
vcos2θa
vsinθ
None
The correct Answer is:A
Step by step video, text & image solution for A particle is moving with constant speed v along the line y = a in positive x -direction. Find magnitude of its angular velocity about orgine when its position makes an angle theta with x-axis. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (GRAVITATION)
25 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Properties of Matter & Fluid Mechanics)(Elasticity)
20 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (COLLISION AND CENTRE OF MASS )
12 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
Similar Questions
A particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle θ=(π2) .
View Solution
Knowledge Check
A particle of mass m is moving with constant speed v on the line y=b in positive x-direction. Find its angular momentum about origin, when position coordinates of the particle are (a, b).
AmvbBmvb/2Cmvb/4DnoneA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is
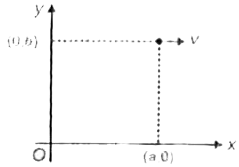 Av√a2+b2BvbCvb(a2+b2)Dva
Av√a2+b2BvbCvb(a2+b2)DvaA particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is
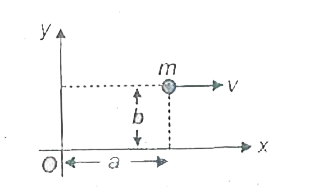 AmvbBmvaCmv√a2+b2Dmv(a+b)
AmvbBmvaCmv√a2+b2Dmv(a+b)
A particle of m=2kg is moving with constant speed 15m/s along a curved path y=x^(2) . Find its angular momentum about origin 0 when its velocity vector is at 53^(@) with x -axis (in kgm^(2)/s)
View SolutionA particle is going parallel to x - axis with constant speed V at a distance 'a' from the axis . Find its angular velocity about an axis passing the origin O , at the instant when radial vector of the particle makes angle θ with the x - axis
View SolutionA particle is moving along a circle with a uniform speed v. Find (a) change in the magnitude of velocity and (b) the magnitude of change in the velocity when it has rotated an angle θ.(0<θ<90∘)
View SolutionA particle is moving in the xy-plane with a constant velocity along a line parallel to the X-axis away from the origin. The magnitude of its angular momentum about the origin.
View SolutionA particle of mass m is moving on the XY-plane along a straight line y = d, with constant velocity v. Its angular momentum about the origin
View Solution
