An ideal diatomic gas is taken through an adiabatic process in which density increases to 32 times. If pressure increases to 'n' times. Find n
4
8
64
128
The correct Answer is:D
To solve the problem, we need to analyze the adiabatic process of an ideal diatomic gas, where the density increases to 32 times its initial value. We will find the factor by which the pressure increases, denoted as 'n'.
1. Understanding the Adiabatic Process:
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between pressure (P), volume (V), and density (ρ) can be described by the equation:
PVγ=constant
where γ (gamma) is the adiabatic index.
2. Relating Density and Volume:
Density is defined as:
ρ=mV
Therefore, we can express volume in terms of density:
V=mρ
3. Substituting Volume in the Adiabatic Equation:
Substitute V in the adiabatic equation:
P(mρ)γ=constant
This can be rearranged to show the relationship between pressure and density:
P∝ργ
Thus, we can write:
PfPi=(ρfρi)γ
4. Given Information:
The problem states that the final density (ρf) is 32 times the initial density (ρi):
ρfρi=32
5. Finding the Value of Gamma for Diatomic Gas:
For a diatomic gas, the value of γ is:
γ=CpCv=75
6. Substituting Values into the Pressure Equation:
Now substitute the values into the pressure equation:
PfPi=(32)75
We can express 32 as 25:
PfPi=(25)75=27=128
7. Conclusion:
Therefore, the pressure increases to 128 times the initial pressure:
n=128
Final Answer:
The value of n is 128.
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between pressure (P), volume (V), and density (ρ) can be described by the equation:
PVγ=constant
where γ (gamma) is the adiabatic index.
Density is defined as:
ρ=mV
Therefore, we can express volume in terms of density:
V=mρ
Substitute V in the adiabatic equation:
P(mρ)γ=constant
This can be rearranged to show the relationship between pressure and density:
P∝ργ
Thus, we can write:
PfPi=(ρfρi)γ
The problem states that the final density (ρf) is 32 times the initial density (ρi):
ρfρi=32
For a diatomic gas, the value of γ is:
γ=CpCv=75
Now substitute the values into the pressure equation:
PfPi=(32)75
We can express 32 as 25:
PfPi=(25)75=27=128
Therefore, the pressure increases to 128 times the initial pressure:
n=128
The value of n is 128.
Topper's Solved these Questions
Similar Questions
Knowledge Check
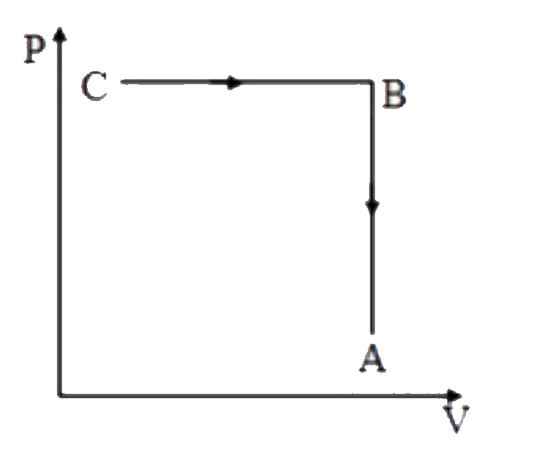
Ideal gas is taken through the process shown in the figure :
 Ain process AB, work done by system is positiveBin process AB, heat is rejectedCin process AB, internal energy increasesDin process AB internal energy decreases and in process BC, internal energy increases.
Ain process AB, work done by system is positiveBin process AB, heat is rejectedCin process AB, internal energy increasesDin process AB internal energy decreases and in process BC, internal energy increases.Ideal gas is taken through process shown in figure
 Aln process AB, work done by system is positiveBIn process AB, heat is rejected out of the system.CIn process AB, internal energy increasesDIn process AB internal energy decreases and
Aln process AB, work done by system is positiveBIn process AB, heat is rejected out of the system.CIn process AB, internal energy increasesDIn process AB internal energy decreases and
in process BC internal energy increasesIdeal gas is taken through process shown in figure :
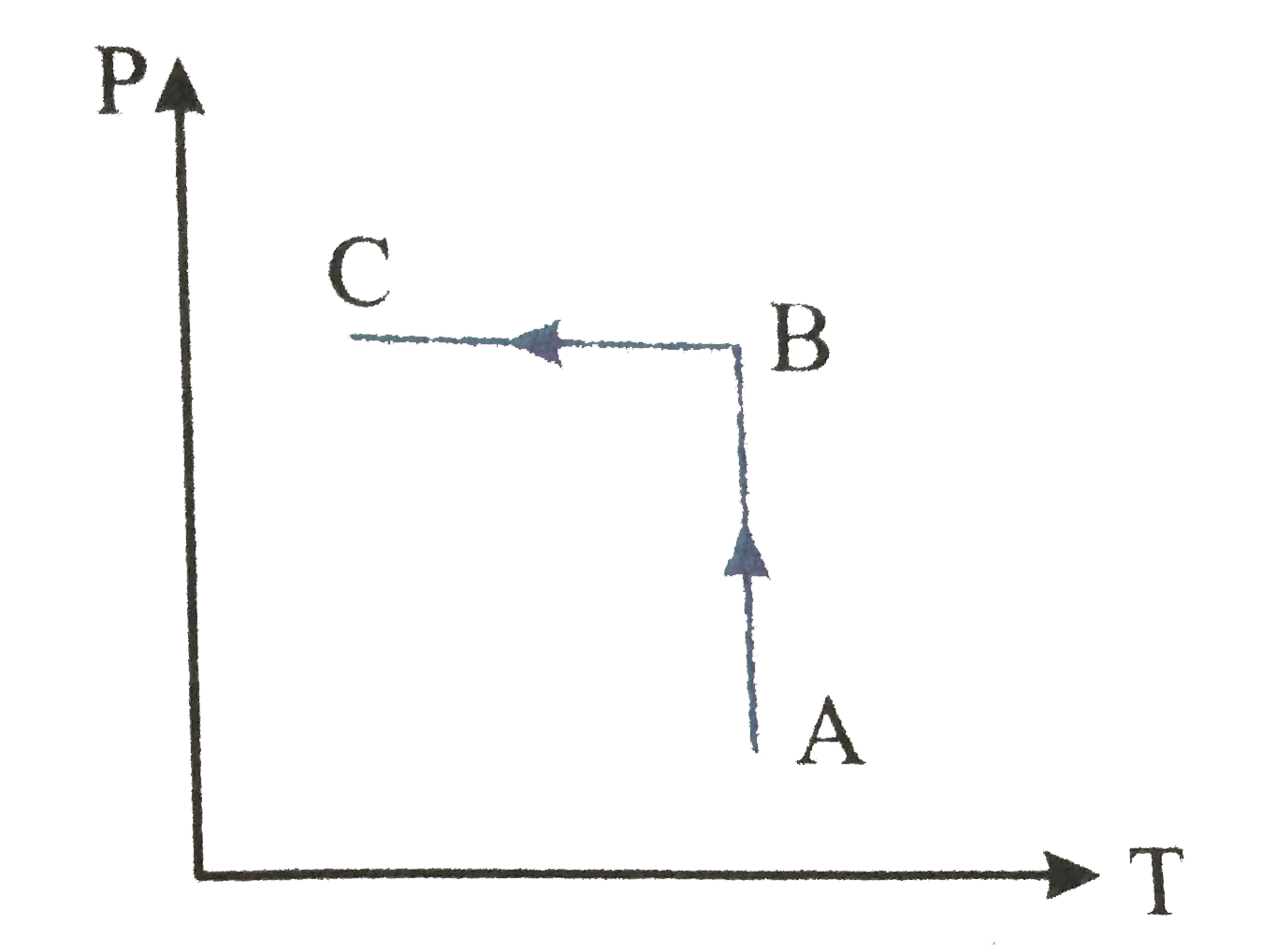
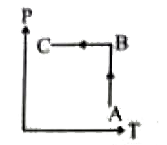 AIn process AB. work done by system is positiveBIn process AB, heat is reacted out of the system.Cprocess AB, internal exergy increasesDIn process AB internal energy decreases and in process BC Internal energy increases.
AIn process AB. work done by system is positiveBIn process AB, heat is reacted out of the system.Cprocess AB, internal exergy increasesDIn process AB internal energy decreases and in process BC Internal energy increases.
An ideal monatomic gas undergoes an adiabatic process , and its internal energy increases by 50 J which pair of choices below is correct for this process ?
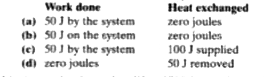
View SolutionA diatomic mass expands adiabatically so that final density is 32 times the initial density. Find pressure becomes N times of initial presurre . the value of N is:
View SolutionOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
View SolutionTwo moles of an ideal diatomic gas is taken through a process VT2= constant so that its temperature increases by ΔT=300K. The ratio (ΔUΔQ) of increase in internal energy and heat supplied to the gas during the process is
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
View Solution