Potential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
r=(6A11B)15
r=(11B6A)15
r=(6B11A)15
r=(11A6B)15
The correct Answer is:B
To find the value of r for the equilibrium position given the potential energy function U=−Ar6+Br11, we will follow these steps:
Step 1: Understand the relationship between potential energy and force
The force F is related to the potential energy U by the equation:
F=−dUdr
At equilibrium, the force must be zero:
F=0⟹−dUdr=0⟹dUdr=0
Step 2: Differentiate the potential energy with respect to r
We need to differentiate U with respect to r:
U=−Ar6+Br11
Using the power rule for differentiation:
dUdr=ddr(−Ar6)+ddr(Br11)
=6Ar−7−11Br−12
Step 3: Set the derivative equal to zero for equilibrium
Now, we set the derivative equal to zero:
6Ar−7−11Br−12=0
Step 4: Rearranging the equation
Rearranging the equation gives:
6Ar−7=11Br−12
Multiplying both sides by r12 to eliminate the negative powers:
6Ar5=11B
Step 5: Solve for r
Now, we can solve for r5:
r5=11B6A
Taking the fifth root of both sides gives:
r=(11B6A)15
Final Answer
Thus, the value of r for the equilibrium position is:
r=(11B6A)15
The force F is related to the potential energy U by the equation:
F=−dUdr
At equilibrium, the force must be zero:
F=0⟹−dUdr=0⟹dUdr=0
We need to differentiate U with respect to r:
U=−Ar6+Br11
Using the power rule for differentiation:
dUdr=ddr(−Ar6)+ddr(Br11)
=6Ar−7−11Br−12
Now, we set the derivative equal to zero:
6Ar−7−11Br−12=0
Rearranging the equation gives:
6Ar−7=11Br−12
Multiplying both sides by r12 to eliminate the negative powers:
6Ar5=11B
Now, we can solve for r5:
r5=11B6A
Taking the fifth root of both sides gives:
r=(11B6A)15
Thus, the value of r for the equilibrium position is:
r=(11B6A)15
Topper's Solved these Questions
Similar Questions
Knowledge Check
Potential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
Ax=0Bx=5Cx=2.5Dx=7.5The potential energy function of a particle is given by U(r)=A2r2−B3r, where A and B are constant and r is the radial distance from the centre of the force. Choose the correct option (s)
AThe equilibrium distance will be r0=2ABBThe equilibrium distance will be r0=3ABCIf the total energy of the particle is B26A, then its radial velocity will vaishh ate r03, where r0 is the equilibrium distanceDIf the total energy of the particle is B26A, then its radial velocity will vanish at r02,where r0 is the equilibrium distance.If potential energy is given by U=ar2−br. Then find out maximum force. (ggiven a=2,b=4)
A−1627NB−3227NC+3227ND+1627N
Assuming θ=π/2 as the zero-energy position of a magnet in a magnetic field, show that the potential energy of a magent can be written as u=−→B.→m. Hence find the stable equilibrium position of a magnet in a magnet in a magnetic field.
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionIf the potential energy of a gas molecules is given by U=Xr4−Yr8 where X and Y are constants and are positive. Calculate the otential energy at equilibrium .
View SolutionIn the given circuit, find the value of R :
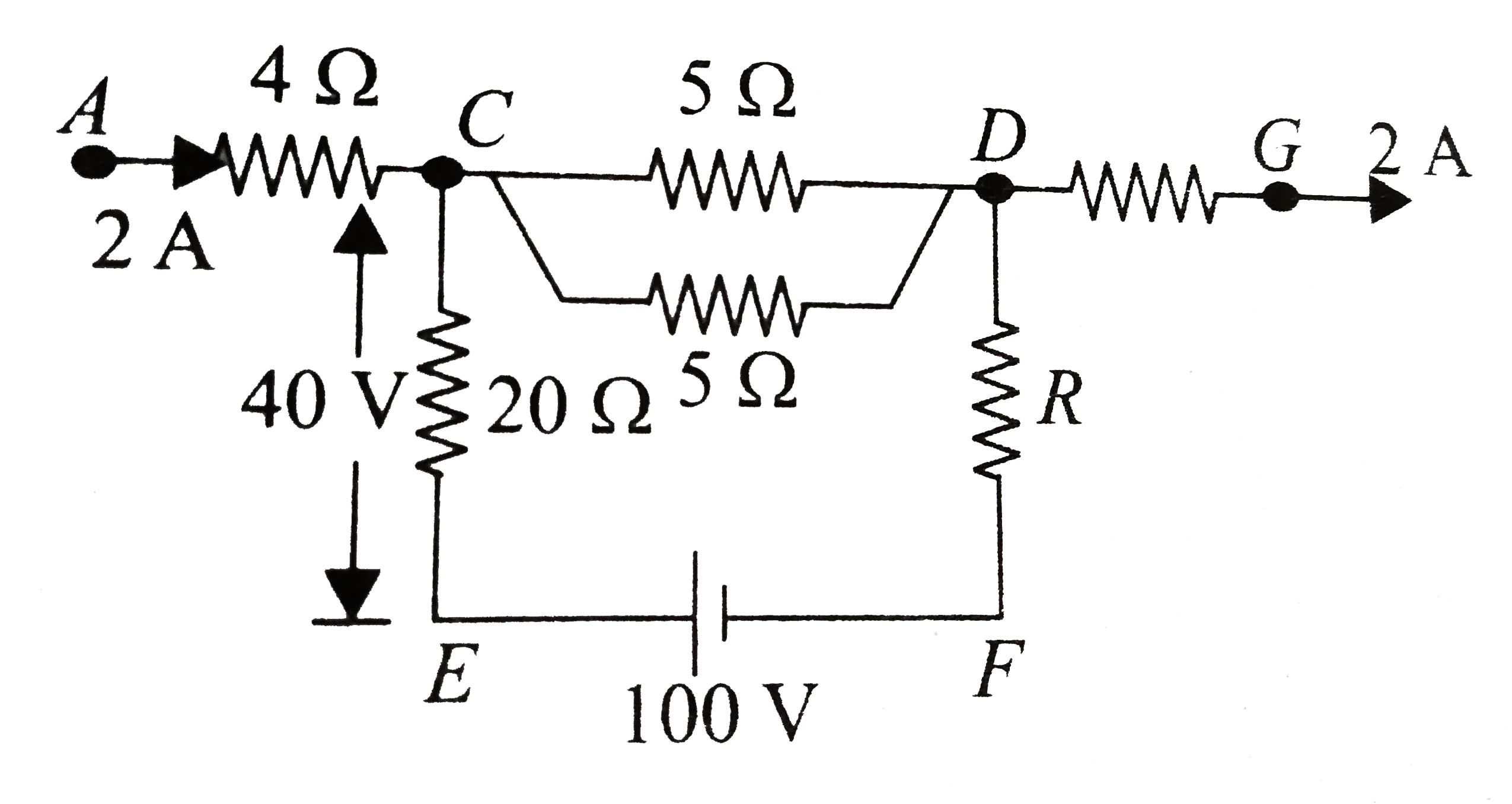 .
.
View SolutionThe potential energy of a particle in a force field is:
U=Ar2−Br,. Where A and B are positive
constants and r is the distance of particle from the centre of the field. For stable equilibrium the distance of the particle is
View Solution

