In ΔPQR,right-angled at Q (see figure), PQ = 3 cm and PR = 6 cm. Determine ∠QPRand ∠PRQ
If we create a right angle triangle ΔPQR with given details,
then,
sinR=PQPR=36=12=sin30∘⇒R=30∘
We know, ∠P+∠Q+∠R=180∘
∠P+90+30=180⇒∠P=180−120=60∘
So,∠QPR=60∘and∠PRQ=30∘
Similar Questions
In ΔOPQ, right-angled at P, OP = 7 cm andOQ − PQ = 1 cmDetermine the values of sin Q and cos Q.
View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
View SolutionIn Fig. 4.230, each of PA, QB, RC and SD is perpendicular to l . If AB=6cm , BC=9cm , CD=12cm and PS=36cm , then determine PQ, QR and RS . (FIGURE)
View SolutionIn ABC and PQR Figure, AB=PQ,BC=QR and CB and RQ are extended to X and Y respectively and ∠ABX =∠PQY. Prove that ABC≅PQR. Figure
View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.

View SolutionIn figure QRQS=QTPRand ∠1=∠2. Show that ΔPQS~ΔTQR.

View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
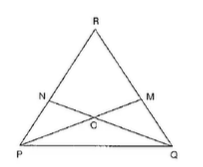
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.

View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.

View Solution