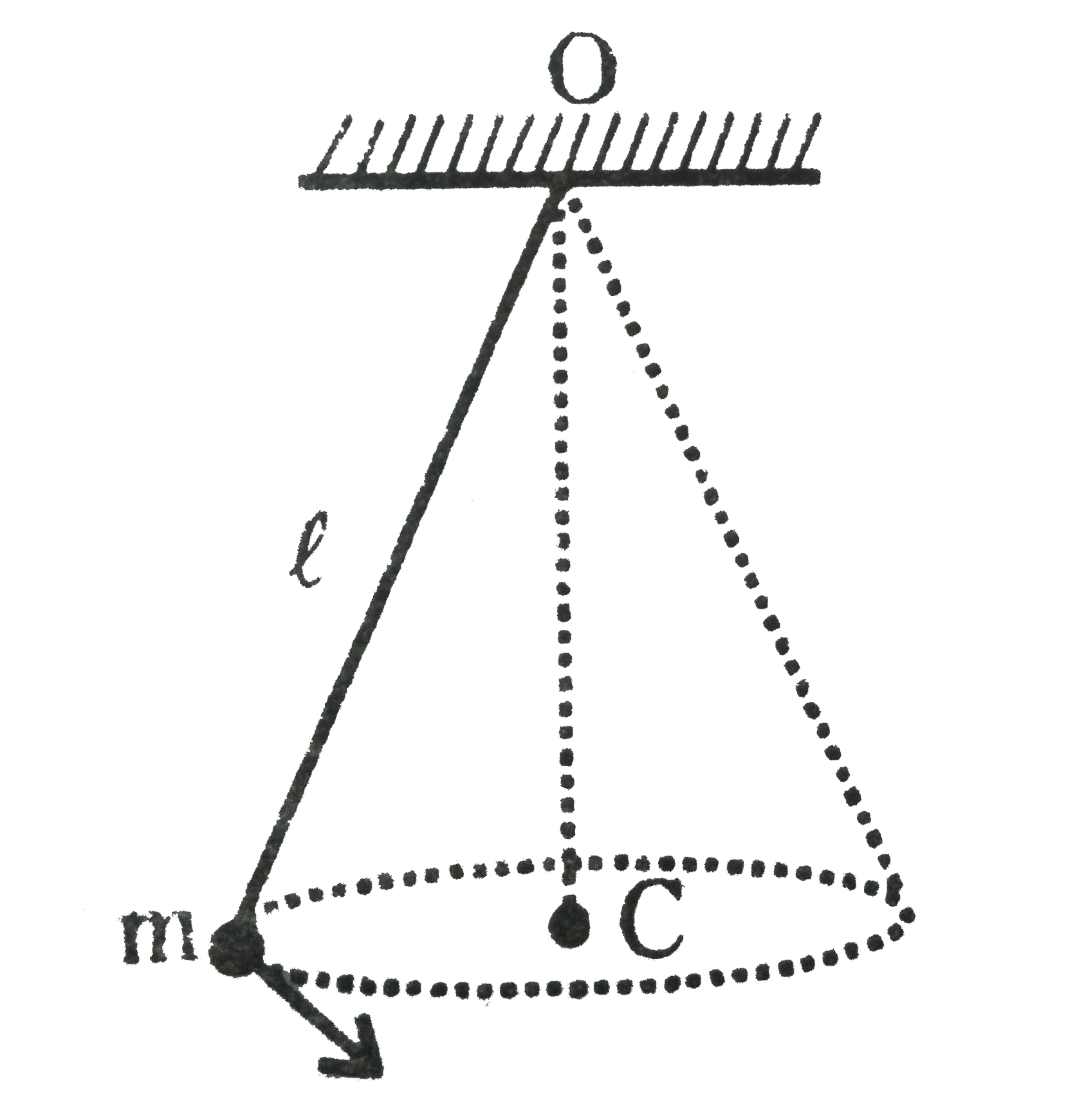
A small charged ball having mass m and charge q is suspended from a rigid support by means of an inextensible thread of length l. It is made to rotate on a horizontal circular path in a uniform, time independent magnetic field of induction B which is directed upward. The time period of revolution of the ball is $T_{0} .$ If the thread is always stretched, calculate the radius of circular path on which the ball moves.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $r = {[L^{2} - {\frac{m g}{m ω^{2} \pm q ω B}}^{2}]}^{1 / 2}$

Charge ball move in the form of conical pendulum.Magnetic force act along radial direction.
$T sin θ = m r ω^{2} \pm q . (r ω) . B$
$T cos θ = m g$
$tan θ = \frac{(m g ω^{2} \pm q ω B) r}{m g}$
$\frac{r}{\sqrt{r^{2} + L^{2}}} = \frac{(m ω^{2} \pm q ω B) r}{m g} \Rightarrow r = {[L^{2} - {\frac{m g}{m ω^{2} \pm q ω B}}^{2}]}^{1 / 2}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
A small ball of mass $m$ suspended from the celling at a point $O$ by a thread of length $l$ moves along a horizontal circle with a constant angular velocity $ω$ .
.
Alinear momentum of system (ball + rod) is conserved
Bangular momentum about C is conserved
Ckinetic energy of system (ball + rod) before the collision is equal to kinetic energy of system just after the collision
Dlinear momentum of ball is conserved
Question 2 - Select One
A simple pendulum of length l is set in motion such that the bob, of mass m, moves along a horizontal circualar path , and the string makes a constant angle $θ$ with the vertical. The time period of rotation of the bob is l and the tension in the thread is T
A $t = 2 π \sqrt{l / g}$
B $t = 2 π \sqrt{l cos θ / g}$
C $T = \frac{4 π^{2} m l}{t^{2}}$
DThe bob is in equilibrium
Question 3 - Select One
Two identical tennis balls each having mass 'm' and charge 'q' are suspended from a fixed point by threads of length 'l'. What is the equilibrium separation when each thread makes a small angle $' θ'$ with the vertical ?
A $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 2}$
B $x = {(\frac{q^{2} l}{2 π ε_{0} m g})}^{1 / 3}$
C $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g})}^{1 / 3}$
D $x = {(\frac{q^{2} l^{2}}{2 π ε_{0} m^{2} g^{2}})}^{1 / 3}$

RESONANCE-ELECTRODYNAMICS-Advanced level problems

Home
Ask Doubt
Profile