For a resistance R and capacitance C in series the impedence is twice that of a parallel combinations of the same elements. The frequency of the applied emf shall be
In case of parallel combination
or
With
So,i.e.,,i.e.,
and as according to given problem,
In case of parallel combination
With
So,i.e.,,i.e.,
i.e.(1+R^(2)omega^(2)C^(2))^(2)=4R^(2)omega^(2)c^(2)or,1+R^(2)omega^(2)C^(2)=2RomegaC(RomegaC-1)^(2)=0oromega=(1)/(RC),i.e.,f=(1)/(2piRC)
Topper's Solved these Questions
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:SOLVED PROBLEMS(OBJECTIVE)prob
Explore 7 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:Exercise
Explore 3 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:(NUMERICAL BASED QUESTIONS)
Explore 4 Videos
Similar Questions
For a resistance R and capacitance C in series the impedance is twice that of a parallel combination of the same elements What is the frequency of applied emf .
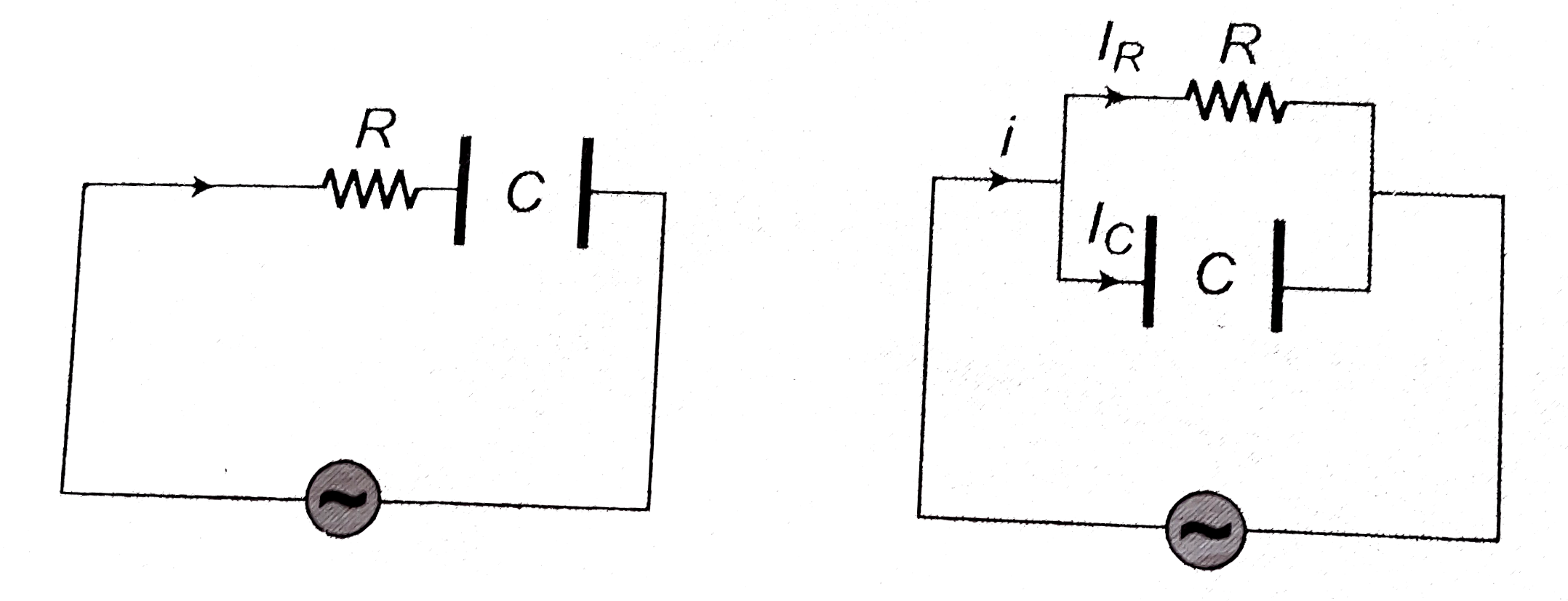 .
.
View SolutionTwo identical cells of emf 1.5V and internal resistance 1Ω are joined in series and the combination is connected in parallel with a third cell of the same emf and internal resistance. Calculalte the terminal voltage of the cells.
View Solution
Knowledge Check
In an A.C. Circuit containing an inductance and a capacitance in series, the current is found to be maximum, when L=0.5H and C=8μF. Then the angular frequency of the applied alternating e.m.f. will be
A25rad/secB500rad/secC750rad/secD1000rad/secAn AC of frequency f is flowing in a circuit containing a resistance R and capacitance C in series. The impedance of the circuit is equal to
AR+fBR+2πfCCR+12πfCD√R2+X2CA capacitor of capacitance 2 μF and resistance of 100 Ω are connected in series and an alternating emf of frequency 1 kHz is applied across the combination. The phase difference between applied emf and current is nearly
A84∘B48∘C38∘D83∘
An LCR series circuit has a resistance of 25 Ω and a reactance of 93.25Ω. If the reactance is capacitive, what is the phase angle between the current and applied emf ? Does the applied emf lag behind or lead the current ?
View SolutionDerive expression for equivalent resistance of a parallel combination of resistances.
(b) Calculate the ratio of equivalent resistance for a series combination of n number of identical resistors to the parallel combination of the same type of n number of resistors.
View SolutionCombination OF Resistance || Series & Parallel Combination || Wheatstone Bridge
View SolutionIn inductance of (4/π) H and the resistor R, are connected in series and an alternating emf of frequency 50 Hz is applied across combination. If phase difference between applied emf and current is 45∘ then the value of R is
View SolutionThe impedance of a sereis RL circuit is same as the series RC circuit when connected to the same AC source separately keeping the same resistance. The frequency of the source is
View Solution