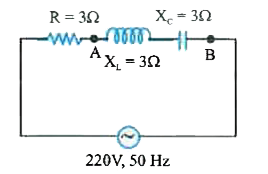
200V A.C. is applied at the ends of an LCR circuit. The circuit consists of an inductive reactance XL=50Ω capacitive reactance Xc=50Ω and ohmic resistance R = 10 Ω . Calculate the impedance of the circuit and also potential differences across L and R What will be the potential difference across L-C
To solve the problem step by step, we will follow the structure of the question and use the given values to find the impedance of the circuit, the potential differences across the components, and the potential difference across the L-C combination.
Step 1: Identify the given values
- Voltage (V) = 200 V
- Inductive reactance (X_L) = 50 Ω
- Capacitive reactance (X_C) = 50 Ω
- Resistance (R) = 10 Ω
Step 2: Calculate the impedance (Z) of the circuit
The impedance of an LCR circuit can be calculated using the formula:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√102+(50−50)2=√100+0=√100=10Ω
Step 3: Calculate the current (I) in the circuit
Using Ohm's law, the current can be calculated as:
I=VZ
Substituting the values:
I=20010=20A
Step 4: Calculate the potential difference across the resistor (V_R)
The potential difference across the resistor can be calculated using:
VR=I⋅R
Substituting the values:
VR=20⋅10=200V
Step 5: Calculate the potential difference across the inductor (V_L)
The potential difference across the inductor can be calculated using:
VL=I⋅XL
Substituting the values:
VL=20⋅50=1000V
Step 6: Calculate the potential difference across the capacitor (V_C)
Since XL=XC, the potential difference across the capacitor can be calculated as:
VC=I⋅XC=20⋅50=1000V
Step 7: Calculate the potential difference across L and C (V_L - V_C)
Since VL and VC are equal, we have:
VL−VC=1000−1000=0V
Step 8: Calculate the potential difference across L and R (V_L - V_R)
The potential difference across L and R can be calculated as:
VL−VR=1000−200=800V
Summary of Results
- Impedance (Z) = 10 Ω
- Potential difference across R (V_R) = 200 V
- Potential difference across L (V_L) = 1000 V
- Potential difference across C (V_C) = 1000 V
- Potential difference across L-C (V_L - V_C) = 0 V
- Potential difference across L-R (V_L - V_R) = 800 V
- Voltage (V) = 200 V
- Inductive reactance (X_L) = 50 Ω
- Capacitive reactance (X_C) = 50 Ω
- Resistance (R) = 10 Ω
The impedance of an LCR circuit can be calculated using the formula:
Z=√R2+(XL−XC)2
Substituting the values:
Z=√102+(50−50)2=√100+0=√100=10Ω
Using Ohm's law, the current can be calculated as:
I=VZ
Substituting the values:
I=20010=20A
The potential difference across the resistor can be calculated using:
VR=I⋅R
Substituting the values:
VR=20⋅10=200V
The potential difference across the inductor can be calculated using:
VL=I⋅XL
Substituting the values:
VL=20⋅50=1000V
Since XL=XC, the potential difference across the capacitor can be calculated as:
VC=I⋅XC=20⋅50=1000V
Since VL and VC are equal, we have:
VL−VC=1000−1000=0V
The potential difference across L and R can be calculated as:
VL−VR=1000−200=800V
- Impedance (Z) = 10 Ω
- Potential difference across R (V_R) = 200 V
- Potential difference across L (V_L) = 1000 V
- Potential difference across C (V_C) = 1000 V
- Potential difference across L-C (V_L - V_C) = 0 V
- Potential difference across L-R (V_L - V_R) = 800 V
Topper's Solved these Questions
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:SOLVED PROBLEMS(OBJECTIVE)prob
Explore 7 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:Exercise
Explore 3 Videos
- AC CIRCUITSBook:FIITJEEChapter:AC CIRCUITSExercise:ASSERTION REASONING TYPE
Explore 1 Video
- COLLISION Book:FIITJEEChapter:COLLISION Exercise:(NUMERICAL BASED QUESTIONS)
Explore 4 Videos
Similar Questions
Knowledge Check
In an experiment, 200V AC is applied at the end of an LCR circuit. The circuit consists of an inductive reactance
(XL) =50Ω, capacitive reactance
(XcL=50Ω, and capacitives resistance
(R)=10Ω, The impendance of the circuit isA10ΩB20ΩC30ΩD40ΩA 200V ac source is applied in a LCR series circuit which consists of an inductive reactance of 50Ω a capacitive reactance of 50Ω and the resistance of 10Ω The potential difference across the resistance is .
A50VB100VC150VD200VIn L-R circuit, resistance is 8Ω and inductive reactance is 6Ω then impedance is:
A2ΩB14ΩC4ΩD10Ω
A series LCR circuit has resistance 10Ω and reactance is 7√2 Ω. What is the impedance of the circuit?
View SolutionIn the given circuit, calculate -

(a) the total resistance of the circuit,
(b) the current through the circuit, and
(c) the potential differences across R1andR2
View SolutionIf the impedance of an L-C R circuit is 40Ω, then the admitance of the circuit will be
View SolutionIf a 16Ωresistance and 12Ω inductive reactance are present in an a.c series circuit. Then the impedance of the circuit will be
View SolutionIn the L-R circuit as shown in figure, potential difference across the resistance at some instant is 4 V. Then
View Solution