In order to get a billiard ball to roll without sliding from the start, where should the cue hit ? Calculate the height from centre of the sphere. Take R as the radius of sphere.
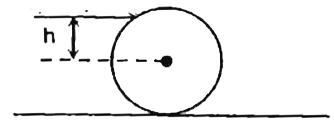
The correct Answer is:2R/5
Step by step video, text & image solution for In order to get a billiard ball to roll without sliding from the start, where should the cue hit ? Calculate the height from centre of the sphere. Take R as the radius of sphere. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (SUBJECTIVE ) LEVEL - II & III
15 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - ASSIGNMENT PROBLEMS (OBJECTIVE ) LEVEL - I
41 Videos
- ROTATIONAL MECHANICSBOOK - FIITJEECHAPTER - ROTATIONAL MECHANICSEXERCISE - EXERCISE
14 Videos
- PHYSICS PART2BOOK - FIITJEECHAPTER - PHYSICS PART2EXERCISE - Numerical Based Question Decimal Type
6 Videos
- SEMICONDUCTOR AND DEVICEBOOK - FIITJEECHAPTER - SEMICONDUCTOR AND DEVICEEXERCISE - SOLVED PROBLEMS Objective: Level-I
20 Videos
Similar Questions
Show that in order to get a billiard ball to roll without sliding from the start the cue must hit the ball not at the center (that is, a height above the table equal to the ball's radius R) but exactly at a height 25R above the center
[Hint, Consider linear momentum and angular motion of the ball. Apply the condtion for rolling without sliding. F = ma and τ=F×h=25mR2×α. Condition rolling without a sliding it a=αR]
View SolutionA uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View Solution
Knowledge Check
Where must the cue hit a billiard ball so that it rolls without sliding form the start if R is the radius of the ball?
AAt a height 25 R above centre.BAt a height equal to the radius from tableCAt a height equal to 2R from the tableDAt a height equal to R2 from table.The potential at a distance R/2 from the centre of a conducting sphere of radius R will be
A0BQ8πε0RCQ4πε0RDQ2πε0RCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 AρπeR2B2ρ0πeR2C3ρ0πeR2D4ρ0πeR2
AρπeR2B2ρ0πeR2C3ρ0πeR2D4ρ0πeR2
A uniform sphere of mass m and radius r rolls without sliding over a horizontal plane, rotating ahout a horizontal axle OA. In the process, the centre of the sphere moves with a veocity v along a circle of radius R. Find the kinetic energy of the sphere.
View SolutionA uniform sphere of radius R16 starts rolling down without slipping from the top of another sphere of radius R=1m. The angular velocity of the sphere of in rads−1, after it leaves the surface of the larger sphere is 8xn. Where n=--
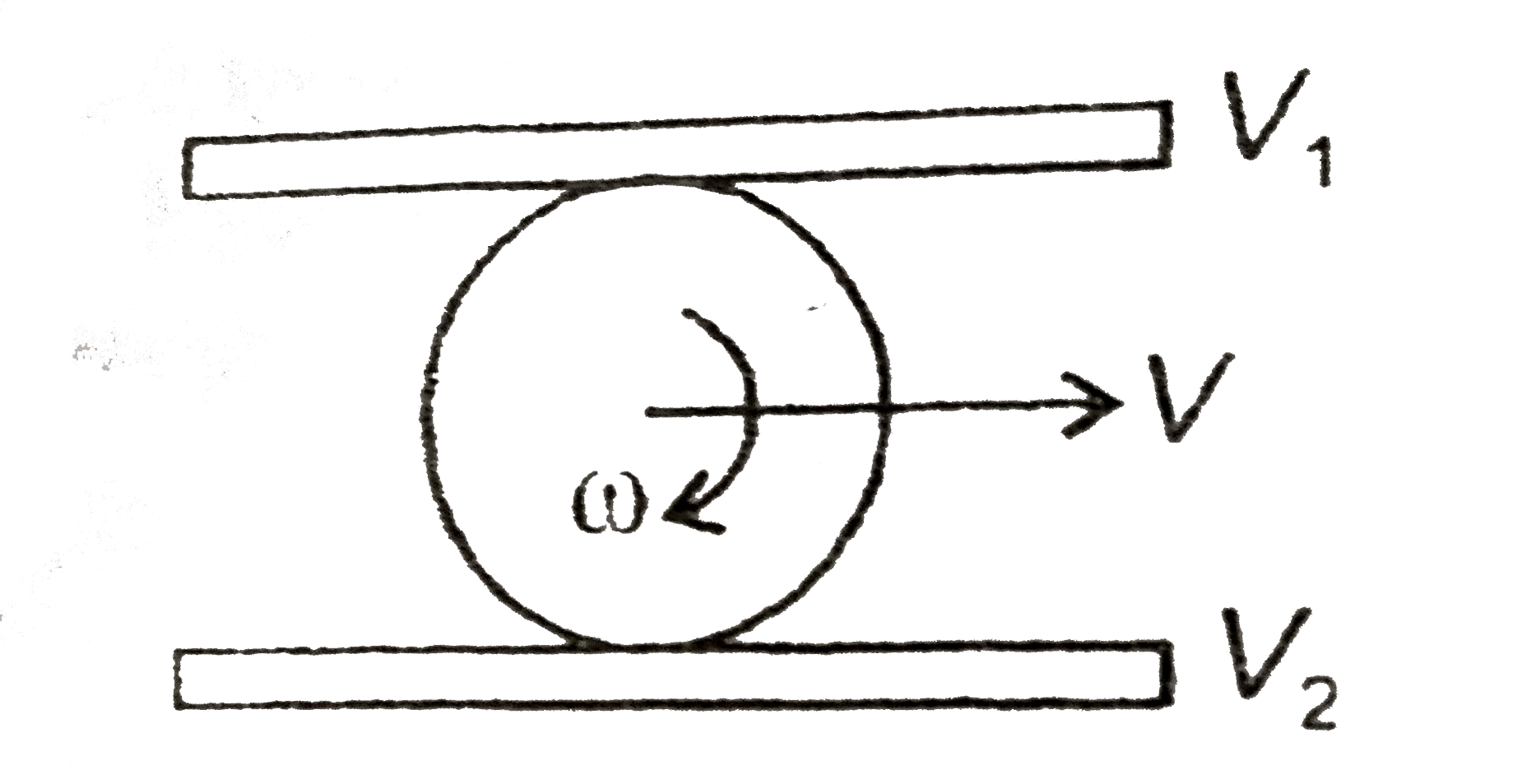
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionA point mass m starts to slide from rest from the top of a smooth solid sphere of radius r. Calculate the angle at which the mass flies off the sphere. If there is friction between the mass and sphere, does the mass fly off at a greater or lesser angle ?
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View Solution
