A particle of mass m is lying at the centre of a solid sphere of mass M and radius R. There is a turnel of negligible thickness, so that particle may escape. Find the minimum velocity required to escape the particle from the gravitational field of the sphere.
The correct Answer is:u=√3GMR
To find the minimum velocity required for a particle of mass m located at the center of a solid sphere of mass M and radius R to escape the gravitational field of the sphere, we can follow these steps:
1. Understanding Gravitational Potential Energy:
The gravitational potential energy U of a mass m at a distance r from the center of a solid sphere of mass M is given by:
U=−3GMm2R
where G is the gravitational constant.
2. Setting Up the Escape Condition:
For the particle to escape the gravitational field, the total mechanical energy (kinetic energy + potential energy) must be greater than or equal to zero:
K.E+U≥0
The kinetic energy K.E of the particle when it has a velocity v is given by:
K.E=12mv2
3. Substituting the Energies:
Substitute the expressions for kinetic energy and potential energy into the escape condition:
12mv2−3GMm2R≥0
4. Simplifying the Equation:
Rearranging the inequality gives:
12mv2≥3GMm2R
Dividing through by m (assuming m≠0):
12v2≥3GM2R
5. Solving for Minimum Velocity:
Multiply both sides by 2:
v2≥3GMR
Taking the square root of both sides gives:
v≥√3GMR
6. Conclusion:
Therefore, the minimum velocity vmin required for the particle to escape the gravitational field of the sphere is:
vmin=√3GMR
The gravitational potential energy U of a mass m at a distance r from the center of a solid sphere of mass M is given by:
U=−3GMm2R
where G is the gravitational constant.
For the particle to escape the gravitational field, the total mechanical energy (kinetic energy + potential energy) must be greater than or equal to zero:
K.E+U≥0
The kinetic energy K.E of the particle when it has a velocity v is given by:
K.E=12mv2
Substitute the expressions for kinetic energy and potential energy into the escape condition:
12mv2−3GMm2R≥0
Rearranging the inequality gives:
12mv2≥3GMm2R
Dividing through by m (assuming m≠0):
12v2≥3GM2R
Multiply both sides by 2:
v2≥3GMR
Taking the square root of both sides gives:
v≥√3GMR
Therefore, the minimum velocity vmin required for the particle to escape the gravitational field of the sphere is:
vmin=√3GMR
Topper's Solved these Questions
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Assigment problems (Objective) (level-I)
Explore 50 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Assigment problems (Objective) (level-I) Assertion & Reasoning type
Explore 2 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Assigment problems (Subjective) (level I)
Explore 14 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
Similar Questions
A particle of mass M is placed at the centre of a uniform spherical shell of equal mass and radius a. Find the gravitational potential at a point P at a distance a2 from the centre.
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
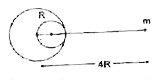
View Solution
Knowledge Check
The escape velocity form the centre of a unifrom ring of mass M and radius R is :
A√2GMRB√GMRC√GM2RD√GMRA particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
A−GmRB−3GmRC−4GmRD−2GmRA particle of mass m is located inside a spherical shell of mass M and radius R. The gravitational force of attraction between them is
AGMmRBGMmR2C−GMmR2D0
A particle of mass M is placed at the centre of a spherical shell of same mass and radius a. What will be the magnitude of the gravitational potential at a point situated at a/2 distance from the centre ?
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA particle of mass M is situated at the centre of a spherical shell of same mass and radius 'a'. The gravitational potential at a point situated at a2 distance from the centre, will be
View SolutionThe escape velocity of a sphere of mass m is given by
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View Solution

