A uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
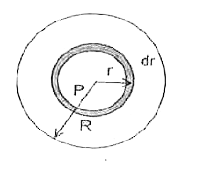
Consider a layer of thickness dr at a distance r from the centre of the sphere.
Now force due to the layer dF=4πr2dP
⇒dPrπr2=G(43πr3ρ)(4πr2drρ)r2
(Where ρ is the mean density of sphere)
or, dP=G43πρ2rdr ∴p=G∫Rr43πρ2rdr
or P=G2π3ρ2(R2−r2)
=38F{1−r2/R2}M2πR4[∴ρ=M/(4/3)πR3]
Topper's Solved these Questions
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Solved problem (Objective)
Explore 15 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Comprehension
Explore 13 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
Similar Questions
Calculate the pressure the pressure caused by gravitational compressions inside the earth , at a distance r from its centre . Take M as the mass of the earth of the earth and R as its radius .
View SolutionThere is a uniform sphere of mass M and radius R. Find the strength G and the potential varϕ of the gravitational field of this sphere as a function of the distance r from its centre (with r<R and r>R). Draw the approximate plots of the functions G(r) and φ(r).
View Solution
Knowledge Check
Inside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
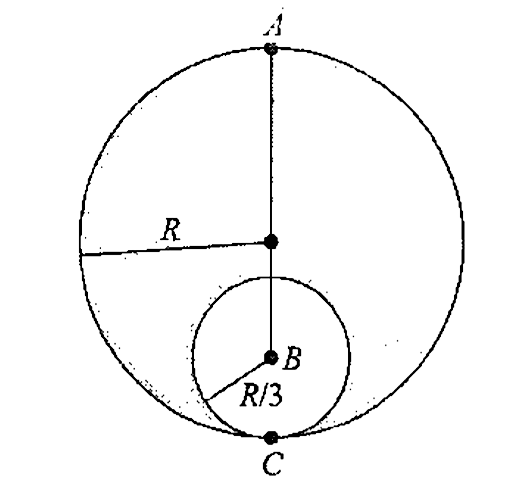 AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system only
AGravitational field inside the cavity is uniformBGravitational field inside the cavity is non-uniformCThe escape velocity of a particle projected from point A is √88GM15RDEscape velocity is defined for earth and particle system onlyTwo spheres each of mass M and radius R are separated by a distance of r. The gravitational potential at the midpoint of the line joining the centres of the spheres is
A−GMrB−2GmrC−GM2rD−4GMrTwo identical spheres each of mass M and Radius R are separated by a distance 10R. The gravitational force on mass m placed at the midpoint of the line joining the centres of the spheres is
AzeroB2GMm25R2CGMm25R2DGMm100R2
A sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
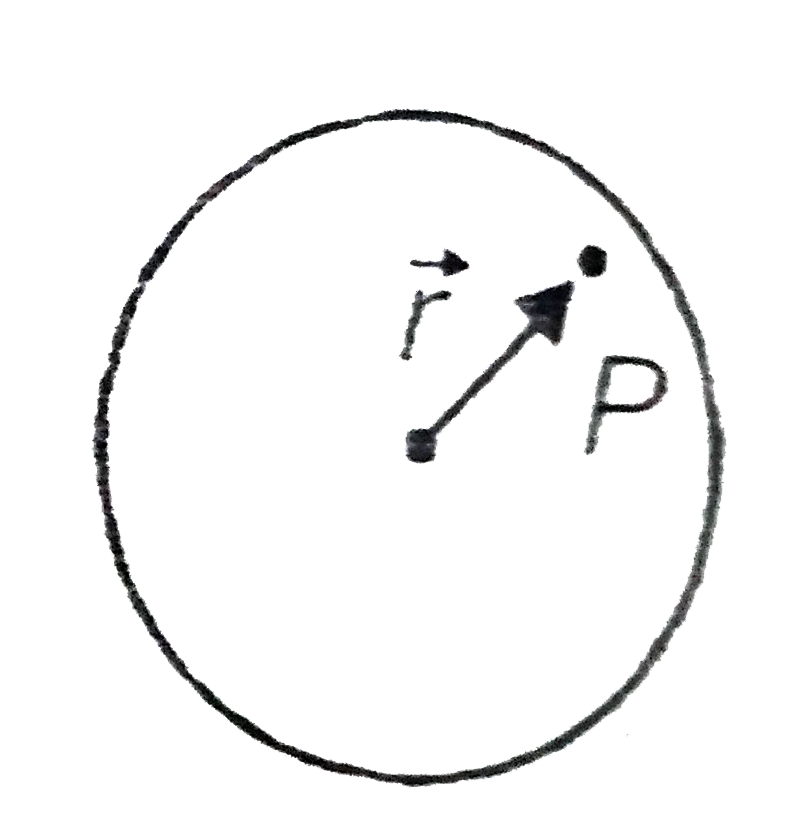
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown

View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solid sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of mass m at a distance R/2 from the centre of the sphere on the line joining both the centre of the cavity)
[Here g=(GM)/R2, where M is the mass of the sphere
View Solution