Space junk of mass $m$ leaves its orbit and heads towards on annular disc-shaped meteor at rest relative to earth along its axis at a distance $8 R$ with a velocity $v$ . The surface mass density of the meteor is $σ$ and its inner and outer radii are $R$ and $4 R$ . Find the velocity with which the junk passes the centre of the meteor. (Thickness of the meteor is negligible).

Video Solution

Text Solution

Verified by Experts

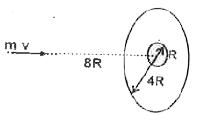
Consider an elemental ring of radius $r$ and width $d r$ .
We have potential energy of the system (ring $+$ junk)
$d E_{1} = - \frac{G m d m}{{(x^{2} + r^{2})}^{1 / 2}} = \frac{G M 2 π d r σ}{{(x^{2} + r^{2})}^{1 / 2}}$
$E_{1} = - 2 π G m σ \int_{R_{1}}^{R_{2}} \frac{r d r}{{(x^{2} + r^{2})}^{1 / 2}}$
Substituting , $x^{2} + r^{2} = t$
$2 r d r = d t$ , $r d r = d t / 2$
$E_{1} = - 2 π G m σ \int \frac{d t}{2 {(t)}^{1 / 2}} = - 2 π G m σ {∣ ∣ {(x^{2} + r^{2})}^{1 / 2} ∣ ∣}_{R_{1}}^{1 / 2}$
$= - 2 π G m s i m g a [{(x^{2} + R_{2}^{2})}^{1 \frac{/}{2}} - {(x^{2} + R_{1}^{2})}^{1 / 2}]$ ......... $(i)$
Ath the centre $E_{2} = - 2 π G m σ (R_{2} - R_{1})$ ......... $(i i)$
The initial kinetic energy of the junk $E_{3} = \frac{1}{2} m v^{2}$
Let the velocity of the junk at the centre be $v .$ then $E_{4} = \frac{1}{2} M v^{2}$
Conserving energy, $E_{1} + E_{3} = E_{2} + E_{4}$
$\Rightarrow - 2 π G m σ [{(x^{2} + R_{2}^{2})}^{1 / 2} - {(x^{2} + R_{1}^{2})}^{1 / 2}] + \frac{1}{2} m v^{2} = - 2 π G m σ (R_{2} - R_{1}) + \frac{1}{2} m v^{2}$
$\Rightarrow - 2 π G σ [{(64 R^{2} + 16 R^{2})}^{1 / 2} - {(64 R^{2} + R^{2})}^{1 / 2}] + \frac{1}{2} v^{2} = - 2 π G σ (3 R) + \frac{1}{2} v .^{2}$
$\Rightarrow v . = {4 π G σ [3 - \sqrt{5} (4 - \sqrt{13})] R + v^{2}}^{1 / 2}$

Updated on:21/07/2023

The moment of inertia of an annular disc of mass M, outer and inner radii R and r, about its diameter is
A $M (R^{2} + r^{2}) / 2$
B $M R^{2}$
C $M r^{2}$
D $M \frac{R^{2} + r^{2}}{4}$
The moment of inertia of an annular disc of mass M, outer and inner radii R and r, about its diameter is
A $M (R^{2} + r^{2}) / 2$
B $M R^{2}$
C $M r^{2}$
D $M \frac{R^{2} + r^{2}}{4}$
Assume the earth's orbit around the sun as circular and the distance between their centres as $D$ Mass of the earth is $M$ and its radius is $R$ if earth has an angular velocity $ω_{0}$ with respect to its centre and $ω$ with respect to the centre of the sun, the total kinetic energy of the earth is:
A $\frac{M R^{2} ω_{0}^{2}}{5} [1 + (\frac{ω}{{(ω_{0})}_{0}^{2}} + \frac{5}{2}) \frac{D ω}{{(R ω_{0})}_{0}^{2}}]$
B $\frac{M R^{2} ω_{0}^{2}}{5} [1 + \frac{5}{2} {(\frac{D ω}{R ω_{0}})}^{2}]$
C $\frac{5}{2} M R^{2} ω_{0}^{2} [1 + \frac{5}{2} {(\frac{D ω}{R ω_{0}})}^{2}]$
D $\frac{2}{5} M R^{2} ω_{0}^{2} [1 + {(\frac{ω}{ω_{0}})}^{2} + \frac{5}{2} {(\frac{D ω}{R ω_{0}})}^{2}]$